Расстояние от прямой до точки – это величина, которая определяет минимальное расстояние между искомой точкой и ближайшей точкой, принадлежащей прямой. Для нахождения этого расстояния необходимо использовать специальную формулу, основанную на уравнении прямой и координатах искомой точки. Расстояние от прямой до точки имеет важное применение в различных областях математики и геометрии, таких как аналитическая геометрия, физика и инженерия.
Расстояние от точки до прямой – определение
Формула расстояния от точки до прямой
Формула расстояния от точки до прямой определяется с использованием векторного произведения, и выглядит следующим образом:
d = |(Ax0 + By0 + C)| / sqrt(A 2 + B 2)
где:
- A, B и C – коэффициенты уравнения прямой вида Ax + By + C = 0;
- (x0, y0) – координаты заданной точки;
- d – искомое расстояние.
Пример нахождения расстояния от точки до прямой
Рассмотрим пример нахождения расстояния от точки до прямой:
Дано уравнение прямой: 2x + 3y – 5 = 0
И заданная точка: (4, -2)
Сначала найдем коэффициенты A, B и C:
A = 2
B = 3
C = -5
Подставляем эти значения в формулу и получаем:
d = |(2*4 + 3*(-2) – 5)| / sqrt(2 2 + 3 2) = |(-1)| / sqrt(13) = 1 / sqrt(13)
Таким образом, расстояние от точки (4, -2) до прямой 2x + 3y – 5 = 0 равно 1 / sqrt(13).
Расстояние от точки до прямой является важным понятием в геометрии и находит применение в различных областях. Формула расстояния позволяет определить минимальное расстояние между заданной точкой и прямой на плоскости. Нахождение этого расстояния может быть полезным при решении задач и построении различных визуализаций.
Лучи и прямые
Расстояние от точки до прямой
Если дана точка и прямая на плоскости, можно вычислить расстояние от точки до прямой. Существует несколько способов найти это расстояние:
- Формула расстояния от точки до прямой: Дана точка с координатами (x,y) и прямая уравнением Ax + By + C = 0. Расстояние (d) от точки до прямой можно вычислить по формуле: d = |Ax + By + C| / √(A 2 + B 2).
- Геометрический способ: Провести перпендикуляр от точки к прямой и измерить его длину.
- Использование векторов: Преобразовать уравнение прямой в векторное уравнение и найти векторное расстояние от точки до прямой.
Примеры расчета расстояния от точки до прямой
Пусть дана прямая с уравнением 2x – 3y + 4 = 0 и точка A(1, 2). Вычислим расстояние от точки A до прямой.
| Шаг | Вычисление |
|---|---|
| 1 | Подставим координаты точки A в уравнение прямой: 2*1 – 3*2 + 4 = 2 – 6 + 4 = 0. |
| 2 | Вычислим расстояние по формуле: d = |2*1 – 3*2 + 4| / √(2 2 + (-3) 2) = |2 – 6 + 4| / √(4 + 9) = 0 / √13 = 0. |
Расстояние от точки A до прямой равно 0. Это означает, что точка лежит на прямой.
Что называется расстоянием от точки до прямой?
Чтобы определить расстояние от точки до прямой, можно использовать различные методы, в зависимости от известных данных и геометрических свойств системы точек и прямых.
Методы определения расстояния от точки до прямой
-
Перпендикулярный спуск
Один из наиболее простых способов определения расстояния от точки до прямой – это построение перпендикуляра из данной точки к прямой. Расстояние равно длине этого перпендикуляра.
Формула для вычисления расстояния от точки с координатами (x₀, y₀) до прямой с уравнением Ax + By + C = 0:
d = |Ax₀ + By₀ + C| / sqrt(A² + B²)
-
Формула расстояния от точки до прямой
Существует также общая формула для определения расстояния от точки до произвольной прямой в пространстве, которая не обязательно должна быть перпендикулярна прямой. Эта формула использует векторы и проекции.
Формула вычисления расстояния от точки A(x₀, y₀, z₀) до прямой, проходящей через точку B(x₁, y₁, z₁) и имеющей направляющий вектор D, записывается следующим образом:
d = |(A – B) × D| / |D|
где × обозначает векторное произведение, |A – B| – длина вектора (A – B), |D| – длина вектора D.
Пример использования в практике
Определение расстояния от точки до прямой имеет множество практических применений. Например:
- В архитектуре и строительстве: определение ближайшей точки для строительства объекта или размещения инфраструктуры;
- В геодезии и картографии: расчет расстояний между точками земной поверхности;
- В компьютерной графике: определение коллизий объектов в 3D-пространстве;
- В оптимизации задач: нахождение оптимального пути или места для размещения;
- В физике и механике: расчет траекторий движения точек относительно прямых линий.
Расстояние от точки до прямой является важным понятием в геометрии и находит применение во многих областях науки и практики.
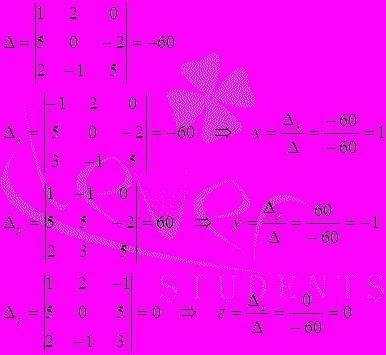
Расстояние между параллельными прямыми
Для нахождения расстояния между параллельными прямыми, вы можете использовать следующую формулу:
Расстояние = |ax + by + c| / √(a 2 + b 2)
Где a, b и c – коэффициенты уравнения прямой Ax + By + C = 0, а x и y – координаты точки, от которой мы измеряем расстояние до параллельной прямой.
В формуле мы сначала вычисляем значение ax + by + c, затем берем его абсолютное значение и делим на квадратный корень из суммы a 2 и b 2.
Используя эту формулу, вы сможете легко находить расстояние между параллельными прямыми и применять его в различных задачах, связанных с геометрией.