Расстояние между точкой и прямой – это одно из основных понятий в математике. Оно определяется как расстояние между данной точкой и ближайшей точкой на прямой. Данная величина имеет большое значение в геометрии и анализе, так как позволяет определить взаимное положение точки и прямой.
Для нахождения расстояния между точкой и прямой необходимо знать координаты данной точки и уравнение прямой. Если уравнение прямой задано в виде y = kx + b, где k – наклон прямой, b – свободный член, то расстояние между точкой и прямой можно найти по формуле:
d = |kx – y + b| / sqrt(k 2 + 1), где d – расстояние, x и y – координаты точки.
Пример
Рассмотрим пример, чтобы лучше понять, как находить расстояние между точкой и прямой. Пусть даны точка А(2, 4) и прямая, заданная уравнением y = 2x + 1. Найдем расстояние между точкой и прямой.
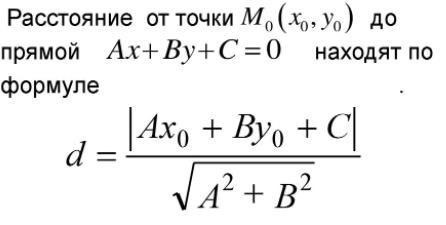
Подставим координаты точки А в формулу для расстояния:
d = |2 * 2 – 4 + 1| / sqrt(2 2 + 1) = |4 – 4 + 1| / sqrt(4 + 1) = 1 / sqrt(5) ≈ 0.45
Таким образом, расстояние между точкой А(2, 4) и прямой y = 2x + 1 составляет примерно 0.45 единицы.
Расстояния между фигурами
1. Расстояние между двумя точками
Наиболее простым случаем является вычисление расстояния между двумя точками в пространстве. Для этого можно воспользоваться формулой расстояния между двумя точками в трехмерном пространстве:
distance = √((x2 – x1) 2 + (y2 – y1) 2 + (z2 – z1) 2)
Где (x1, y1, z1) и (x2, y2, z2) – координаты двух точек в пространстве. Эта формула основана на теореме Пифагора.
2. Расстояние между окружностями
Для вычисления расстояния между окружностями можно воспользоваться следующим алгоритмом:
- Найдите расстояние между центрами окружностей с помощью формулы из предыдущего раздела.
- Если расстояние между центрами меньше, чем сумма радиусов окружностей, то они пересекаются и расстояние между ними равно нулю.
- Если расстояние между центрами равно сумме радиусов окружностей, то они касаются друг друга и расстояние между ними также равно нулю.
- Если расстояние между центрами больше, чем сумма радиусов окружностей, то расстояние между ними равно разности между расстоянием между центрами и суммой радиусов.
3. Расстояние между прямоугольниками
Вычисление расстояния между прямоугольниками может быть сложнее и зависит от их положения и размеров. Один из способов вычисления расстояния между прямоугольниками – это нахождение ближайших точек на границах прямоугольников и вычисление расстояния между этими точками с помощью формулы из первого раздела.
Итог
Расстояние между фигурами – это важное понятие в геометрии, которое имеет множество применений. В данной статье мы рассмотрели вычисление расстояния между различными фигурами, такими как точки, окружности и прямоугольники. Знание этих способов вычисления позволяет решать задачи связанные с определением расстояний между различными геометрическими объектами.