Физические и геометрические понятия широко используются в науке и технике. Одним из важных понятий является расстояние между скрещивающимися прямыми в пространстве. Это расстояние играет ключевую роль при анализе различных конструкций и расчетах.
Расстояние между скрещивающимися прямыми может быть определено с использованием формулы. Для этого необходимо знать координаты точек, через которые проходят прямые, а также угол между ними.
Формула расчета расстояния между скрещивающимися прямыми:
Расстояние = |(X₂ – X₁) * sin(α)|
,где:
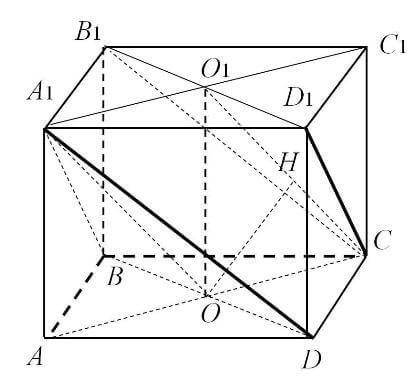
- X₁ и X₂ – координаты точек, через которые проходят прямые
- α – угол между прямыми
- |…| – модуль числа, обозначающий его абсолютное значение
- sin – синус угла
Расстояние может быть положительным или отрицательным, в зависимости от положения точек относительно прямых. Если расстояние равно нулю, это означает, что прямые пересекаются. Если расстояние меньше нуля, это означает, что прямые скрещиваются вне заданного отрезка.
Пример расчета:
Допустим, у нас есть две прямые, проходящие через точки (2, 3, 5) и (4, 7, 1) соответственно. Угол между прямыми составляет 45 градусов. Подставим значения в формулу:
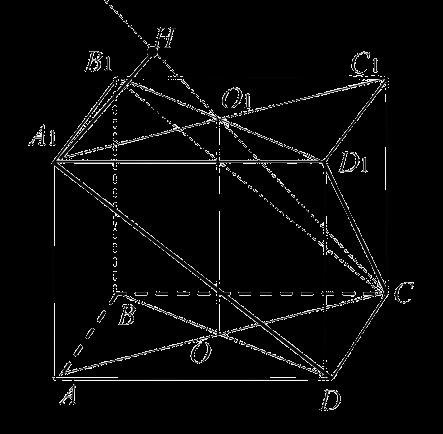
Расстояние = |(4 – 2) * sin(45)|
Расстояние = |2 * sin(45)|
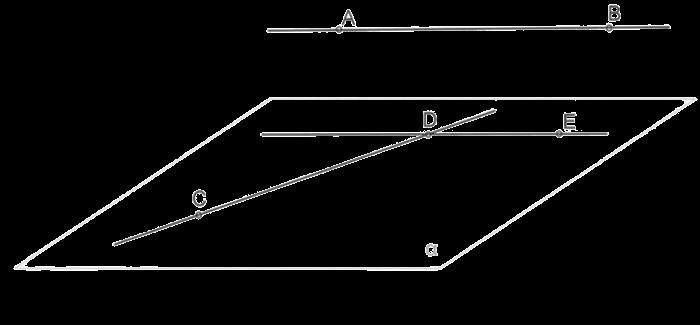
Расстояние ≈ 2.828
Таким образом, расстояние между скрещивающимися прямыми в данном примере составляет около 2.828.

Подписи к слайдам:
В этой статье мы рассмотрели расстояние между скрещивающимися прямыми в пространстве. Мы начали с определения скрещивающихся прямых и изучения их свойств. Затем мы рассмотрели методы вычисления расстояния между ними, включая геометрические и аналитические подходы.
Мы также рассмотрели примеры применения этих методов в задачах геометрии и инженерии. Они включали нахождение расстояния между двумя прямыми в пространстве, определение пересечения прямых и нахождение точек, лежащих на прямых и отстоящих от них на определенное расстояние.
Итак, мы видим, что расстояние между скрещивающимися прямыми в пространстве является важным понятием в геометрии и имеет различные практические применения. Используя геометрические и аналитические методы, мы можем легко вычислить это расстояние и решить разнообразные задачи, связанные с прямыми в пространстве.