Расстояние между плоскостью и прямой – это одна из основных задач в геометрии. Данная задача сводится к вычислению расстояния между точкой и плоскостью, а затем нахождению минимального расстояния от прямой до этой точки. Понимание данной концепции является ключевым для решения различных задач и применения геометрии в реальных ситуациях.
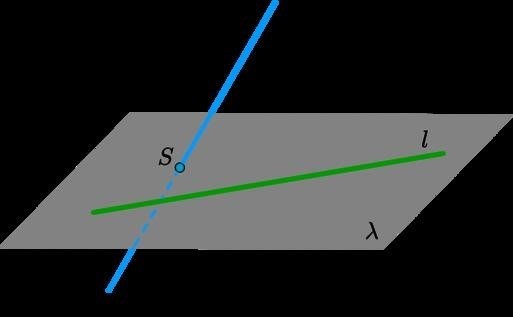
Теорема о трёх перпендикулярах
Формулировка теоремы:
В любом треугольнике существует три перпендикуляра, проведенных из вершин треугольника к серединам противоположных сторон. Эти три перпендикуляра пересекаются в одной точке, центре вписанной окружности треугольника.
Доказательство:
- Проведем перпендикуляр из вершины A треугольника ABC к середине противоположной стороны BC. Обозначим точку пересечения этого перпендикуляра с окружностью как M.
- Проведем перпендикуляр из вершины B к середине противоположной стороны AC. Обозначим точку пересечения этого перпендикуляра с окружностью как N.
- Проведем перпендикуляр из вершины C к середине противоположной стороны AB. Обозначим точку пересечения этого перпендикуляра с окружностью как P.
Точки M, N и P являются серединами радиусов вписанной окружности треугольника ABC.
Свойства теоремы:
- Центр вписанной окружности треугольника является точкой пересечения трех перпендикуляров, проведенных из вершин треугольника к серединам противоположных сторон.
- Радиусы вписанной окружности, проведенные из центра вписанной окружности к сторонам треугольника, являются перпендикулярами к этим сторонам.
- Длины отрезков, соединяющих вершины треугольника с точками пересечения перпендикуляров с окружностью, равны.
Применение теоремы в практике:
Теорема о трех перпендикулярах широко используется в геометрии для решения различных задач, связанных с треугольниками и окружностями. Например, с ее помощью можно найти центр и радиус вписанной окружности треугольника, а также найти радиус отдельных частей этой окружности.
| Пример задачи: | Решение: |
|---|---|
| Найти радиус вписанной окружности треугольника ABC. | Провести перпендикуляры из вершин треугольника к серединам противоположных сторон и найти точку их пересечения – центр вписанной окружности. Радиус вписанной окружности будет равен расстоянию от центра этой окружности до любой из вершин треугольника. |
Теорема о трех перпендикулярах играет важную роль в геометрии и имеет множество практических применений.
Определения расстояний между объектами в пространстве
1. Расстояние между двумя точками
Расстояние между двумя точками в трехмерном пространстве может быть найдено с использованием формулы расстояния между точками. Данная формула основывается на теореме Пифагора и выражается следующим образом:
Формула:
d = sqrt((x2 – x1) 2 + (y2 – y1) 2 + (z2 – z1) 2)
2. Расстояние между прямой и точкой
Расстояние между прямой и точкой в трехмерном пространстве может быть найдено с использованием формулы расстояния от точки до прямой. Данная формула выражается следующим образом:
Формула:
d = |(Ax + By + C) / sqrt(A 2 + B 2)|
3. Расстояние между двумя параллельными плоскостями
Расстояние между двумя параллельными плоскостями может быть найдено с использованием формулы расстояния между точкой и плоскостью. Данная формула основывается на нормальном векторе плоскости и выражается следующим образом:
Формула:
d = |(Ax + By + Cz + D) / sqrt(A 2 + B 2 + C 2)|
4. Расстояние между прямой и плоскостью
Расстояние между прямой и плоскостью в трехмерном пространстве может быть найдено с использованием формулы, основанной на расстоянии от точки до плоскости. Данная формула выражается следующим образом:
Формула:
d = |(Apx + Bpy + Cpz + Dp) / sqrt(A 2 + B 2 + C 2)|
Вышеописанные формулы позволяют находить расстояния между различными объектами в трехмерном пространстве. Зная эти формулы, можно решать широкий спектр задач, связанных с геометрией и пространственными отношениями.
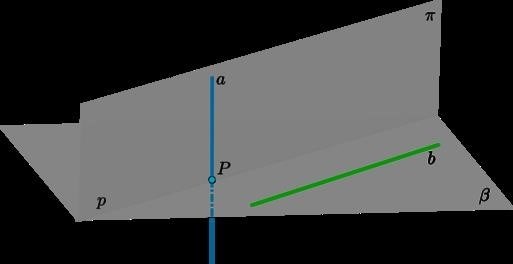
Расстояние между прямой и параллельной ей плоскостью: определение
Определение расстояния между прямой и параллельной ей плоскостью
Расстояние между прямой и параллельной ей плоскостью может быть рассчитано с использованием различных методов и формул. Одним из наиболее распространенных и простых способов является использование векторов.
Для определения расстояния между прямой и параллельной ей плоскостью, можно взять произвольную точку на плоскости и построить вектор, проведенный от этой точки до прямой. Затем, с использованием данного вектора и направляющих векторов прямой и плоскости, можно вычислить проекцию вектора на плоскость.
Полученная проекция вектора на плоскость будет являться вектором, имеющим начало в точке на прямой и перпендикулярной плоскости. Затем можно использовать свойства векторов и геометрическую интерпретацию иными методами, чтобы вычислить длину данного вектора, которая будет являться искомым расстоянием между прямой и параллельной ей плоскостью.
Пример использования формулы
Пусть дана прямая с параметрическим представлением:
Линия: $$L: begin{cases} x = x_0 + at \ y = y_0 + bt \ z = z_0 + ct end{cases}$$
Дано также уравнение плоскости, параллельной прямой:
Плоскость: $$P: Ax + By + Cz + D = 0$$
Для определения расстояния между линией и плоскостью, можно выбрать произвольную точку $$(x_0, y_0, z_0)$$ на линии и использовать формулу:
$$d = frac{sqrt{A 2 + B 2 + C 2}}$$
где d – расстояние между линией L и плоскостью P.
Важность расстояния между прямой и параллельной ей плоскостью
Расстояние между прямой и параллельной ей плоскостью играет важную роль в различных областях. Например, в инженерии и архитектуре это понятие помогает определить оптимальное расположение объектов или сконструировать точные и надежные конструкции. В физике расстояние между прямой и плоскостью может использоваться для расчета векторов сил или определения точек наибольшего напряжения.
Нахождение расстояния между параллельными прямой и плоскостью
В данной статье мы рассмотрели различные способы нахождения расстояния между параллельными прямой и плоскостью. Эта задача встречается в различных областях математики и физики, и ее решение может быть полезным для практических задач.
Мы начали с определения расстояния между точкой и плоскостью, и затем перешли к нахождению расстояния между прямой и плоскостью. Рассмотрели два основных подхода – геометрический и аналитический.
В геометрическом подходе мы использовали параллельные прямые и построение перпендикуляров, чтобы найти расстояние между прямой и плоскостью. В аналитическом подходе мы использовали координаты и уравнения плоскости и прямой, чтобы найти расстояние.
Также мы рассмотрели несколько примеров, чтобы лучше понять, как применять данные методы. Более подробно изучили случаи, когда прямая параллельна плоскости и когда она наклонена к плоскости.
Итак, задача по нахождению расстояния между параллельными прямой и плоскостью может быть решена как с помощью геометрических методов, так и с использованием аналитических выкладок. Выбор метода зависит от предпочтений и самой задачи.