Прямой код, обратный код и дополнительный код являются различными способами представления чисел в компьютере. Прямой код представляет число без изменений, обратный код получается инвертированием каждого бита в прямом коде, а дополнительный код получается прибавлением единицы к обратному коду. Эти коды используются для выполнения арифметических операций с отрицательными числами и представления значений разрядной сетки. Каждый из этих кодов имеет свои преимущества и недостатки, и их выбор зависит от конкретных требований и задач при работе с данными.
Прямой код: определение и особенности
Основные принципы прямого кода:
- Использование только неотрицательных чисел
- Введение дополнительного разряда для обозначения знака
- При использовании битов для представления чисел, каждый бит обычно представляет определенный вес или значение
Пример прямого кода:
Для более наглядного представления начислим весам битам значения. Пусть крайний левый бит (разряд) отвечает за знак, а остальные разряды – за значения от 2 2 до 2 0 (от старшего к младшему разряду). Рассмотрим следующий пример:
| Знак | 2 2 | 2 1 | 2 0 |
|---|---|---|---|
| + | 0 | 1 | 1 |
В таблице представлено число в прямом коде, где знак “+” обозначен 0, а значения разрядов равны 1.
Использование прямого кода
Прямой код применяется для числовых представлений в различных сферах компьютерной науки, включая арифметические операции, хранение данных, процессорные операции и т.д. Благодаря использованию знакового разряда, прямой код позволяет точно определить положительные и отрицательные значения чисел в электронных системах.

В целом, прямой код – это один из методов представления целых чисел, используемый в компьютерах и схожий с дополнительным кодом и обратным кодом. Его особенностью является добавление знакового бита для обозначения отрицательных чисел.
Где всё это применять
Программирование
Одним из главных областей, где применяется прямой код, обратный код и дополнительный код, является программирование. Эти коды используются для выполнения различных операций с числами, таких как сложение, вычитание, умножение и деление. Знание этих кодов помогает программистам эффективно работать с целочисленными данными и обрабатывать их в своих программах.
Криптография
В криптографии прямой код, обратный код и дополнительный код используются для шифрования и расшифровки данных. Эти коды обеспечивают безопасность передаваемой информации и защиту от несанкционированного доступа. Знание этих кодов позволяет специалистам в области криптографии создавать защищенные системы обмена информацией.
Машинное обучение
В машинном обучении применение прямого кода, обратного кода и дополнительного кода может быть связано с представлением данных и обработкой числовых значений. Эти коды могут использоваться для кодирования информации и выполнения различных операций в алгоритмах машинного обучения. Знание этих кодов позволяет ученым в области машинного обучения эффективно работать с данными и достигать лучших результатов в своих исследованиях.
Компьютерные сети
Прямой код, обратный код и дополнительный код также применяются в компьютерных сетях для передачи данных. Эти коды позволяют эффективно представлять числовую информацию при передаче по сети и обеспечивают ее надежность и целостность. Знание этих кодов важно для сетевых инженеров и специалистов по информационной безопасности.
Видеоигры
В индустрии видеоигр применение прямого кода, обратного кода и дополнительного кода может быть связано с обработкой и представлением графических данных. Эти коды позволяют разработчикам создавать реалистичные и эффектные визуальные эффекты, а также оптимизировать работу игровых движков. Знание этих кодов помогает инженерам по программному обеспечению создавать качественные и интересные игры.
Прямой, обратный и дополнительный коды
Прямой код
Прямой код представляет число в обычной двоичной форме с учетом знака. Например, положительное число 5 может быть представлено в прямом коде как 0101, а отрицательное число -5 будет иметь прямой код 1011.
Обратный код
Обратный код получается инвертированием всех битов числа в прямом коде, кроме знакового бита. Например, для числа 5 его обратный код будет 1010, а для -5 – 0100.
Дополнительный код
Дополнительный код получается при добавлении единицы к обратному коду. Таким образом, число -5 в дополнительном коде будет представлено как 0101 + 1 = 0110.
Сравнение кодов
- Прямой код является наиболее простым способом представления чисел, но не удобен для выполнения арифметических операций.
- Обратный код удобен для выполнения операций сложения и вычитания, но требует дополнительных операций при выполнении других арифметических операций.
- Дополнительный код является наиболее удобным для выполнения всех арифметических операций, так как при сложении и вычитании чисел в дополнительном коде не требуется особых действий.
Прямой, обратный и дополнительный коды представляют различные способы работы с отрицательными числами в компьютерной арифметике. Дополнительный код является наиболее удобным и широко используется при выполнении арифметических операций.
Практическая часть
В данном разделе мы рассмотрим практическую часть работы с прямым кодом, обратным кодом и дополнительным кодом. Ниже приведены основные пункты, которые мы рассмотрим:
1. Конвертация из прямого кода в обратный код
Конвертация числа из прямого кода в обратный код может выполняться путем выполнения следующих шагов:
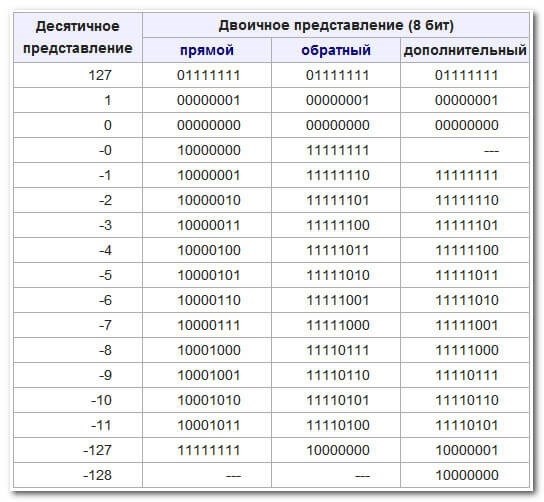
- Проверить знак числа
- Инвертировать все биты числа
- Добавить к результату единицу
2. Конвертация из обратного кода в прямой код
Для конвертации числа из обратного кода в прямой код необходимо выполнить следующие действия:
- Проверить знак числа
- Выполнить инверсию всех битов числа
- Добавить к результату единицу
3. Конвертация из прямого кода в дополнительный код
Для конвертации числа из прямого кода в дополнительный код нужно выполнить следующие шаги:
- Проверить знак числа
- Инвертировать все биты числа
- Добавить к результату единицу
4. Конвертация из дополнительного кода в прямой код
Конвертация числа из дополнительного кода в прямой код может быть выполнена следующим образом:
- Проверить знак числа
- Выполнить инверсию всех битов числа
- Добавить к результату единицу
| Число | Прямой код | Обратный код | Дополнительный код |
|---|---|---|---|
| -5 | 11111011 | 10000100 | 10000101 |
| 7 | 00000111 | 00000111 | 00000111 |
| -10 | 11110110 | 10001001 | 10001010 |
Как видно из примеров, прямой, обратный и дополнительный коды числа могут различаться в зависимости от его знака. Важно правильно выполнять конвертацию между этими кодами для корректной работы с числами в компьютерных системах.
Обратный код
Определение и формат
Обратный код представляет собой способ записи отрицательного числа, при котором его биты инвертируются (меняются на противоположные). Знак числа обозначается самым старшим (левым) битом, где 1 обозначает отрицательное число, а 0 – положительное.
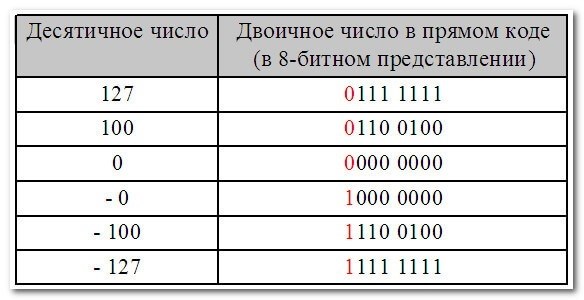
Формат обратного кода может варьироваться в зависимости от используемой системы. В некоторых системах дополнительный бит (дополнительная единица) добавляется к числу перед инверсией битов, чтобы избежать проблемы с представлением нуля. В других системах дополнительный бит заменяется наивысшим (старшим) битом, который сохраняет свое значение.
Операции с обратным кодом
Операции с числами в обратном коде выполняются путем преобразования чисел в прямой код, выполнения операции, после чего результат может быть преобразован обратно в обратный код. Например, для сложения двух чисел в обратном коде, необходимо выполнить сложение и проверить переносы для корректировки результата.
Применение обратного кода
Обратный код широко применяется в компьютерной архитектуре, особенно в арифметических операциях, чтобы выполнить операции с отрицательными числами. Обратный код также используется при представлении чисел с плавающей точкой или встроенных операций с плавающей точкой.
Преимущества и недостатки
Преимущества:
- Более простое представление отрицательных чисел по сравнению с дополнительным кодом.
- Простота выполнения арифметических операций в обратном коде.
Недостатки:
- Более сложное представление нуля и проверка переносов при выполнении операций.
- Неоднозначность представления некоторых чисел (например, положительного и отрицательного нуля).
В целом, обратный код является важным инструментом для работы с отрицательными числами в компьютерных системах, который обладает своими преимуществами и недостатками. Понимание его принципов и особенностей помогает разработчикам и архитекторам создавать эффективные и надежные вычислительные системы.
Модифицированные обратные и дополнительные коды
Для представления отрицательных чисел в компьютерных системах используются различные коды, включая прямой код, обратный код и дополнительный код. Каждый из них имеет свои особенности и предназначен для определенных целей. Рассмотрим модифицированные обратные и дополнительные коды.
Модифицированный обратный код
Модифицированный обратный код является разновидностью обратного кода. В нем изменена интерпретация самого левого бита числа, обычно используемого для обозначения знака. Вместо того, чтобы использовать его как обычный знаковый бит (1 для отрицательных чисел, 0 – для положительных), в модифицированном обратном коде этот бит используется для обозначения нуля. Таким образом, отрицательные числа имеют самый левый бит, равный 1, а положительные числа имеют самый левый бит, равный 0.

Такая модификация обратного кода позволяет упростить операции сложения и вычитания, поскольку для их выполнения нет необходимости выполнять операции с самым левым битом. Это делает модифицированный обратный код более удобным в использовании и экономит время при выполнении арифметических операций.
Модифицированный дополнительный код
Модифицированный дополнительный код является улучшенной версией дополнительного кода. В дополнительном коде для отрицательных чисел самый левый бит равен 1, а для положительных чисел – 0. Однако в модифицированном дополнительном коде самый левый бит отличается в зависимости от значения символа числа: для 0 он равен 0, для отрицательного числа – 1, для положительного числа – 0.
Это позволяет упростить операции сложения и вычитания, так как в модифицированном дополнительном коде нет необходимости в выполнении дополнительных операций с самым левым битом. Кроме того, модифицированный дополнительный код обеспечивает две нулевые разряды, что делает его более надежным и точным при выполнении арифметических операций.
Арифметические действия в машинных кодах
В машинных кодах арифметические действия осуществляются с использованием различных методов, таких как прямой код, обратный код и дополнительный код. Каждый из этих методов имеет свои особенности и применяется в различных ситуациях.
Прямой код
Прямой код представляет числа в обычном двоичном виде. Этот метод наиболее простой, но имеет свои недостатки. Например, он не учитывает знак числа. Поэтому при выполнении арифметических операций с числами в прямом коде может возникнуть проблема с определением знака результата.
Обратный код
Обратный код представляет отрицательные числа в виде инвертированных двоичных разрядов и добавления 1 к полученному результату. Это позволяет избежать проблемы с определением знака результата при выполнении арифметических операций. Однако, обратный код требует дополнительных операций для выполнения арифметических действий.

Дополнительный код
Дополнительный код является наиболее удобным и распространенным методом представления чисел в машинных кодах. Он представляет отрицательные числа в виде инвертированных двоичных разрядов и добавления 1 к полученному результату, как и обратный код. Однако, дополнительный код имеет дополнительное преимущество – он позволяет выполнять арифметические операции с использованием обычных операций сложения и вычитания, не требуя дополнительных операций.
Таким образом, арифметические действия в машинных кодах выполняются с использованием разных методов, таких как прямой код, обратный код и дополнительный код. Каждый из этих методов имеет свои особенности и применяется для решения определенных задач. Дополнительный код представляет наиболее удобный способ выполнения арифметических операций, так как не требует дополнительных операций и позволяет использовать обычные арифметические операторы.
Зачем всё это знать
Применение прямого, обратного и дополнительного кодов находит свое применение во многих областях, таких как:
- Арифметика с фиксированной точкой: эти коды позволяют нам работать и выполнять операции с числами, хранимыми в форме дробных числителей;
- Обработка знаковых чисел: дополнительный код позволяет нам выполнить отрицательные числа в компьютерных системах, что является необходимым для работы с отрицательными значениями в различных приложениях;
- Максимальная и минимальная представимые числа: знание кодов помогает нам определить минимальное и максимальное представимые числа в компьютерных системах;
- Коррекция ошибок и обнаружение ошибок: эти коды используются для обнаружения и исправления ошибок в передаче данных.
В целом, знание прямого кода, обратного кода и дополнительного кода является важным фактором для разработчиков программного обеспечения, компьютерных инженеров и всех, кто работает с числами в цифровой форме. Это позволяет эффективнее использовать вычислительные ресурсы, улучшить точность и надежность вычислений и создать оптимизированные алгоритмы для работы с числами.