При изучении геометрии одним из важных свойств треугольника является пропорциональность его сторон к синусам противолежащих углов. Это свойство позволяет проводить различные вычисления и расчеты, а также определять различные характеристики треугольника.
Для начала, давайте рассмотрим определение синуса угла. Синус угла в треугольнике определяется как отношение длины противолежащей стороны к гипотенузе.
Таким образом, если у нас есть треугольник ABC, где углы α, β и γ являются углами треугольника, а BC, AC и AB – стороны треугольника, то имеем следующие пропорции:
- Синус угла α = BC / AC
- Синус угла β = AC / AB
- Синус угла γ = AB / BC
Теперь, зная эти пропорции, мы можем проводить различные вычисления на основе данных треугольника. Например, если нам известны длины двух сторон треугольника и величина противолежащего угла, мы можем найти длину третьей стороны при помощи синуса этого угла.
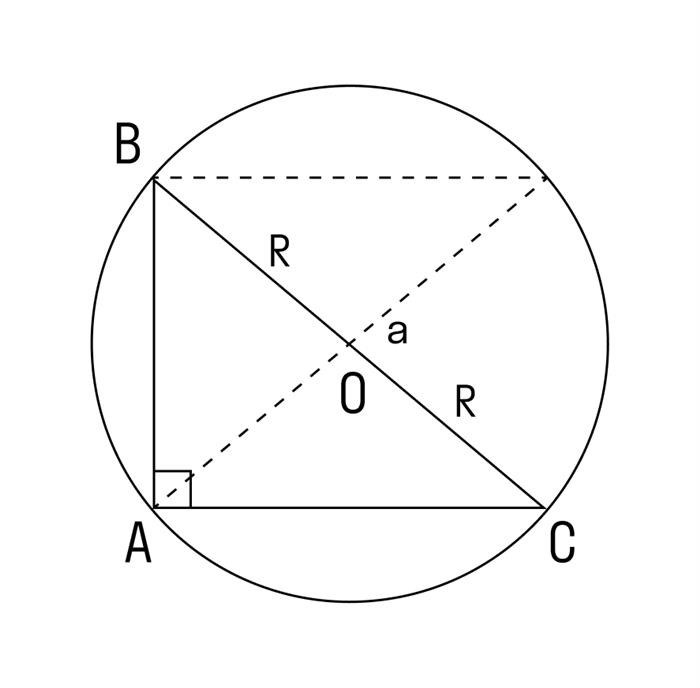
Также, используя пропорции синусов углов, мы можем определить, является ли треугольник прямоугольным. Если сумма квадратов синусов двух прямых углов равна 1, то треугольник является прямоугольным.
Примеры и решения
В данной статье мы рассмотрели свойство, согласно которому стороны треугольника пропорциональны синусам противолежащих углов. Давайте рассмотрим несколько конкретных примеров и решим их.
Пример 1:
Дан треугольник ABC, где угол A равен 30°, сторона AB равна 6 см, а сторона BC равна 8 см. Необходимо найти сторону AC.
Решение:
Известно, что сторона AB пропорциональна синусу угла C, а сторона BC пропорциональна синусу угла A. Так как синус угла A равен 0.5 (sin30° = 0.5), а сторона AB равна 6 см, можно определить пропорцию:
AB/BC = sinA/sinC
Подставим известные значения:
6/8 = 0.5/sinC
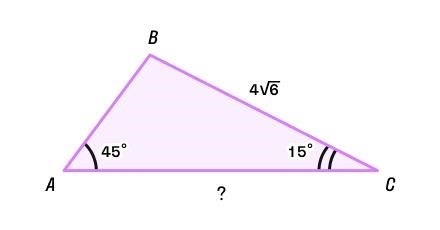
Сокращаем дробь и умножаем на sinC:
3/4 = sinC
Используя обратную функцию синуса, получаем значение угла C:
C = arcsin(3/4)
Значение этого угла можно взять из таблицы значений или использовать калькулятор. В данном случае C ≈ 48.59°.
Используя теорему синусов, находим сторону AC:
AC = AB/sinB * sinC
Подставляем известные значения:
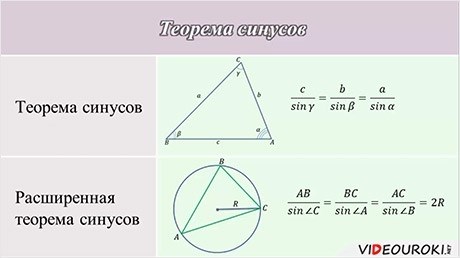
AC = 6/sin30° * sin48.59°
Вычисляем значения синусов и проводим необходимые арифметические операции:
AC ≈ 12.25 см
Пример 2:
Дан треугольник PQR, где угол Q равен 45°, сторона PQ равна 5 м, а сторона QR равна 10 м. Необходимо найти сторону PR.
Решение:
Аналогично предыдущему примеру, используем теорему синусов:
PQ/QR = sinQ/sinR
Подставляем известные значения:

5/10 = sin45°/sinR
Упрощаем дробь и соответственно синусы:
1/2 = sinR
Используя обратную функцию синуса, получаем значение угла R:
R = arcsin(1/2)
Значение этого угла можно взять из таблицы значений или использовать калькулятор. В данном случае R ≈ 30°.
Используя теорему синусов, находим сторону PR:
PR = PQ/sinP * sinR

Подставляем известные значения:
PR = 5/sin90° * sin30°
Вычисляем значения синусов и проводим необходимые арифметические операции:
PR ≈ 7.07 м
Обобщая, можно сказать, что использование теоремы о пропорциональности сторон треугольника с синусами углов является эффективным методом для решения задач на нахождение неизвестных сторон треугольника, основываясь на известных углах и сторонах.