Произведение любого числа на нулевой вектор всегда дает в результате нулевой вектор. Это свойство является одним из основных в линейной алгебре и при решении математических задач обладает важным значением.
Следствия аксиом линейного пространства
Следствие 1: Произведение любого числа на нулевой вектор есть нулевой вектор
Одной из аксиом линейного пространства является свойство ассоциативности умножения числа на вектор. Это значит, что умножение числа на вектор можно ассоциировать с операцией умножения чисел:
λ(μv) = (λμ)v
Исходя из этого свойства, можно вывести следствие: произведение любого числа на нулевой вектор всегда будет равно нулевому вектору. Это может быть интерпретировано следующим образом:
- Если вектор представляет какое-либо физическое состояние, то умножение его на ноль будет означать полное отсутствие этого состояния;
- Если вектор является результатом некоторой операции, то умножение его на ноль будет означать, что эта операция не имеет эффекта;
- Произведение любого числа на нулевой вектор можно рассматривать как уникальный случай обнуления вектора.
Следствие 2: Произведение нуля на любой вектор также есть нулевой вектор
Из свойств линейного пространства также следует, что произведение нуля на любой вектор также будет равно нулевому вектору:
0v = 0
Это следствие возникает из определения умножения числа на вектор и аксиомы, которая утверждает, что существует нейтральный элемент (ноль) относительно операции сложения в линейном пространстве.
Следствие 3: Сумма нулевого вектора и произвольного вектора равна этому вектору
В линейном пространстве также существует аксиома о наличии нулевого элемента относительно операции сложения:
v + 0 = v
Из этой аксиомы следует, что сумма нулевого вектора и произвольного вектора будет равна этому вектору:
0 + v = v
Это следствие можно интерпретировать следующим образом:
- Сложение вектора с нулевым вектором не меняет значений исходного вектора;
- Нулевой вектор является “нейтральным” элементом относительно операции сложения, так как при его сложении с любым вектором результат не изменяется.
Популярные статьи за последние 7 дней
В течение последних семи дней были опубликованы несколько статей, которые привлекли большой интерес читателей. В этом обзоре мы расскажем о некоторых из них.
Останетесь в курсе самых актуальных тем, узнайте о новых открытиях и тенденциях в различных областях знаний.
1. “Один из самых важных открытий в области медицины”
Одной из самых важных статей за последнюю неделю стала публикация о новом медицинском открытии. Исследователи изучили влияние некоторых веществ на процесс возникновения и развития определенных заболеваний. Результаты исследования позволяют надеяться на разработку новых методов лечения и предупреждения определенных патологий в ближайшем будущем.
2. “Революционный подход к решению проблемы энергетики”
Вторая статья, о которой стоит упомянуть, посвящена проблеме энергетики и инновационным методам ее решения. Исследователи предложили новую концепцию, основанную на использовании возобновляемых источников энергии. Этот подход может стать революционным и помочь справиться с проблемой истощения традиционных источников энергии.
3. “Новые перспективы в области искусственного интеллекта”
Искусственный интеллект – одна из наиболее актуальных тем современности. В третьей статье за последние 7 дней авторы представили новые перспективы в области искусственного интеллекта. Они исследовали возможности применения нейронных сетей и глубокого обучения для решения сложных задач. Полученные результаты открывают новые горизонты для применения искусственного интеллекта в различных сферах жизни, от медицины до транспорта.
4. “Вынесен новый приговор в известном уголовном деле”
Важным событием, которое не оставило равнодушными многих, стало завершение известного уголовного дела. В четвертой статье за последнюю неделю рассказывается о расследовании преступления, о его следствии и назначенном судом приговоре. Это дело имеет большое общественное значение и вызывает много дискуссий.
5. “Новые тренды в мире моды”
Самая свежая информация о модных трендах представлена в пятой статье. Авторы изучили последние коллекции высоких модных брендов и выбрали самые интересные и актуальные тенденции сезона. Будьте в тренде и следуйте модным веяниям.
Это лишь небольшая часть популярных статей, опубликованных за последние 7 дней. Если вы хотите быть в курсе новых открытий и событий, следите за актуальными публикациями.
Свойства произведения вектора на число
1. Простейшее свойство произведения вектора на число
Одним из самых простых свойств произведения вектора на число является то, что если умножить вектор на ноль, то результатом будет нулевой вектор. Это свойство следует из определения операции умножения и является фундаментальным в линейной алгебре.
2. Линейность произведения вектора на число
Произведение вектора на число обладает свойством линейности, что означает, что результат умножения вектора на сумму двух чисел равен сумме произведений вектора на каждое из этих чисел. Формально это можно записать следующим образом:
k * (a + b) = k * a + k * b,
где k – число, a и b – векторы.
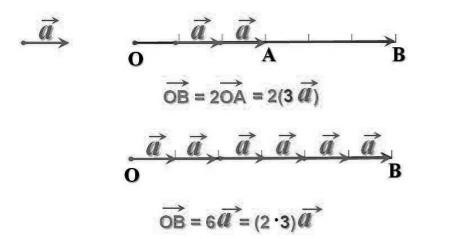
3. Ассоциативность произведения вектора на число
Важным свойством произведения вектора на число является ассоциативность, то есть порядок умножения вектора на несколько чисел не влияет на итоговый результат. Формально это можно записать следующим образом:
(k1 * k2) * a = k1 * (k2 * a),
где k1 и k2 – числа, a – вектор.
4. Дистрибутивность произведения вектора на число
Произведение вектора на число обладает свойством дистрибутивности относительно сложения векторов. Это означает, что умножение вектора на сумму двух чисел равно сумме произведений вектора на каждое из этих чисел. Формально это можно записать следующим образом:
k * (a + b) = k * a + k * b,
где k – число, a и b – векторы.
5. Обратное произведение вектора на число
Обратное произведение вектора на число возможно, если это число не равно нулю. В этом случае, если умножить вектор на обратное число, то результатом будет вектор, противоположный по направлению и пропорциональный по длине исходному вектору:
k * a = a / k = -a,
где k – число, a – вектор.
| Свойство | Формула |
|---|---|
| Простейшее свойство произведения вектора на число | k * 0 = 0 |
| Линейность произведения вектора на число | k * (a + b) = k * a + k * b |
| Ассоциативность произведения вектора на число | (k1 * k2) * a = k1 * (k2 * a) |
| Дистрибутивность произведения вектора на число | k * (a + b) = k * a + k * b |
| Обратное произведение вектора на число | k * a = a / k = -a |
Примеры линейных пространств
Пространство векторов
Пространство векторов – это множество всех векторов, имеющих специальные свойства. Векторы могут быть двумерными, трехмерными и т.д. Каждый вектор может быть представлен в виде упорядоченной совокупности чисел. Примеры пространств векторов: геометрические пространства (двумерное, трехмерное и др.), пространство всех многочленов, пространство всех непрерывных функций и др.
Матричное пространство
Матричное пространство – это множество всех матриц одного и того же размера, над некоторым полем. Матрицы можно складывать и умножать на число, а также умножать друг на друга. Примеры матричных пространств: пространство всех квадратных матриц, пространство всех симметричных матриц, пространство всех диагональных матриц и др.
Пространство функций
Пространство функций – это множество всех функций, определенных на некотором множестве. Функции можно складывать и умножать на число. Примеры пространств функций: пространство всех непрерывных функций, пространство всех дифференцируемых функций, пространство всех интегрируемых функций и др.
Пространство полиномов
Пространство полиномов – это множество всех полиномов. Полиномы можно складывать и умножать на число. Примеры пространств полиномов: пространство всех полиномов степени не выше n, пространство всех многочленов с вещественными коэффициентами и др.
Пространство последовательностей
Пространство последовательностей – это множество всех последовательностей чисел, обладающих специальными свойствами. Последовательности можно складывать и умножать на число. Примеры пространств последовательностей: пространство всех ограниченных последовательностей, пространство всех сходящихся последовательностей и др.
Пространство математических объектов
Пространство математических объектов – это множество всех математических объектов, обладающих определенными свойствами. Примеры пространств математических объектов: пространство всех графов, пространство всех вещественных чисел, пространство всех множеств и др.
Итоги
Мы узнали, что при умножении вектора на число, длина вектора увеличивается или уменьшается в зависимости от значения этого числа. Если число положительное, то вектор увеличивается в размере, если отрицательное – уменьшается. Если же число равно нулю, то результатом умножения будет нулевой вектор.
Также, мы рассмотрели основные свойства умножения вектора на число:
- Коммутативность: умножение числа на вектор дает тот же результат, что и умножение вектора на число;
- Ассоциативность: умножение вектора на произведение двух чисел равно произведению каждого из чисел на вектор;
- Дистрибутивность: сумма двух векторов, умноженных на число, равна сумме каждого из векторов, умноженных на это число.
Таким образом, умножение вектора на число является важной операцией, применяемой в различных областях, таких как физика, геометрия, экономика и др. На основе свойств этой операции строятся и доказываются различные математические теоремы и алгоритмы.