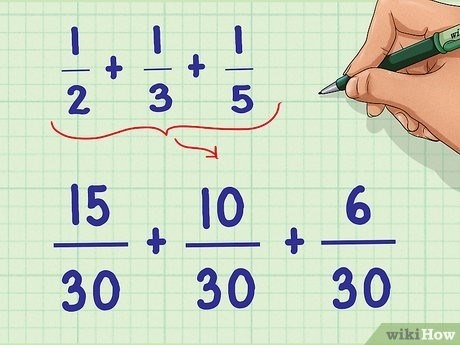
Приведение дробей к общему знаменателю – это процесс преобразования дробей таким образом, чтобы у них был одинаковый знаменатель. Это важное математическое действие, которое помогает сравнивать и складывать дроби. В статье будет рассмотрено несколько методов, которые позволяют сделать это проще и эффективнее.
Как найти общий знаменатель дробей
1. Метод наименьших общих кратных (НОК)
НОК – это наименьшее число, которое делится без остатка на все знаменатели дробей. Чтобы найти общий знаменатель с помощью НОК:
- Найдите НОК знаменателей всех дробей.
- Умножьте каждую дробь на такое число, чтобы её знаменатель стал равным НОК.
Например, если у нас есть дроби 1/3 и 2/5, то НОК для знаменателей 3 и 5 равен 15. Мы умножаем 1/3 на 5/5 и получаем 5/15, а 2/5 умножаем на 3/3 и получаем 6/15. Теперь оба знаменателя равны 15, и мы можем выполнять операции с этими дробями.
2. Метод простого умножения
Если знаменатели дробей являются простыми числами, общий знаменатель можно найти, умножив эти числа. Например, если у нас есть дроби 1/2 и 2/3, то общий знаменатель будет равен 2 * 3 = 6. Мы умножаем 1/2 на 3/3 и получаем 3/6, а 2/3 умножаем на 2/2 и получаем 4/6. Теперь оба знаменателя равны 6, и мы можем проводить операции с этими дробями.
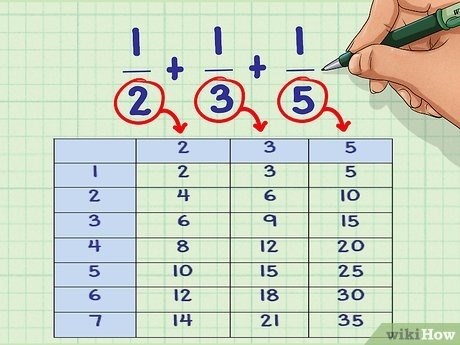
3. Метод таблицы умножения
Если знаменатели дробей не являются простыми числами, можно воспользоваться методом таблицы умножения. Чтобы найти общий знаменатель с помощью таблицы умножения:
- Найдите все простые числа, на которые делится каждый знаменатель дробей.
- Для каждого простого числа вычислите его наибольшую степень, которая делится без остатка на знаменатель.
- Общий знаменатель будет равен произведению всех простых чисел, возведенных в соответствующие степени.
Например, если у нас есть дроби 1/4 и 3/8, то знаменатели 4 и 8 делятся на простое число 2. 4 = 2 2, а 8 = 2 3. Общий знаменатель будет равен 2 3 = 8. Мы умножаем 1/4 на 2/2 и получаем 2/8, а 3/8 оставляем без изменений. Теперь оба знаменателя равны 8, и мы можем проводить операции с этими дробями.
Что мы узнали?
В процессе изучения темы о приведении дробей к общему знаменателю мы узнали ряд важных концепций и методов, которые помогут нам решать подобные задачи.
1. Общий знаменатель
Общий знаменатель – это знаменатель, который является общим для всех дробей, которые мы хотим привести к нему. Для того чтобы найти общий знаменатель, мы можем использовать несколько методов:
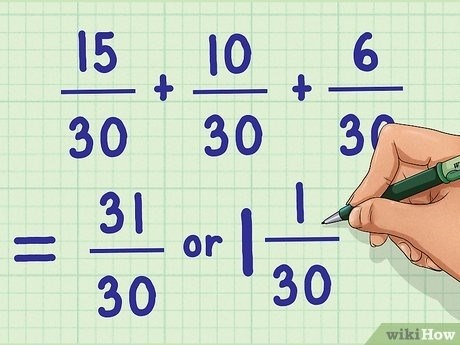
- Наименьшее общее кратное (НОК)
- Умножение знаменателей дробей
- Использование алгоритма Евклида
2. Приведение дробей
Приведение дробей к общему знаменателю позволяет нам работать с ними однородным образом. Для этого мы можем использовать следующие методы:
- Умножение числителя и знаменателя каждой дроби на одно и то же число
- Использование расширенного алгоритма Евклида
3. Применение приведения дробей
Применение приведения дробей к общему знаменателю в решении задач помогает нам упростить их и получить более точный ответ. Например, это может быть полезно при решении задач по алгебре, физике, экономике и других дисциплинах. Приведение дробей дает нам возможность сравнивать, складывать и вычитать дроби, а также выполнять другие арифметические операции с ними.
4. Распространенные ошибки
Распространенные ошибки при приведении дробей к общему знаменателю могут включать следующие:
- Неправильное нахождение общего знаменателя
- Неверное приведение дроби
- Ошибки в вычислениях
| Дробь | Знаменатель | Приведенная дробь |
|---|---|---|
| 1/2 | 6 | 3/6 |
| 3/4 | 6 | 4/6 |
В ходе изучения этой темы мы поняли, что приведение дробей к общему знаменателю является важным инструментом для работы с дробями. Он позволяет нам сравнивать, складывать и вычитать дроби, а также выполнять другие операции с ними. Нахождение общего знаменателя и приведение дробей к нему являются основными шагами в решении задач, где требуется работа с дробями.
Что такое дробь?
Примеры дробей:
- 1/2 – одна половина
- 3/4 – три четверти
- 2/3 – две трети
Дроби могут быть представлены в различных форматах: простые, смешанные, правильные и неправильные.
| Формат | Пример | Объяснение |
|---|---|---|
| Простая дробь | 3/5 | Числитель меньше знаменателя |
| Смешанная дробь | 2 3/4 | Целая часть и дробная часть |
| Правильная дробь | 2/3 | Числитель меньше знаменателя |
| Неправильная дробь | 5/4 | Числитель больше знаменателя |
Важные понятия связанные с дробями:

- Числитель – верхняя часть дроби, показывает количество частей
- Знаменатель – нижняя часть дроби, показывает количество равных частей
- Десятичная дробь – дробь, где знаменатель равен 10, 100 и т.д.
- Сокращение дроби – сведение числителя и знаменателя к общему делителю
Знание и понимание дробей важно в различных областях, таких как финансы, наука, строительство и другие. Разные операции с дробями могут быть выполнены с помощью приведения дробей к общему знаменателю, чтобы их можно было сравнивать и складывать.
Важно помнить, что дроби являются неотъемлемой частью математики и имеют широкое практическое применение в реальном мире.
Зачем нужно находить общий знаменатель?
Нахождение общего знаменателя в дробях играет важную роль при выполнении различных математических операций, таких как сложение, вычитание и сравнение дробей. Общий знаменатель позволяет привести дроби к одинаковому виду, что упрощает их сравнение и анализ.
При сложении или вычитании дробей общий знаменатель позволяет сравнивать и комбинировать их числители. Если дроби имеют разные знаменатели, они должны быть приведены к общему знаменателю, чтобы можно было выполнять арифметические операции.
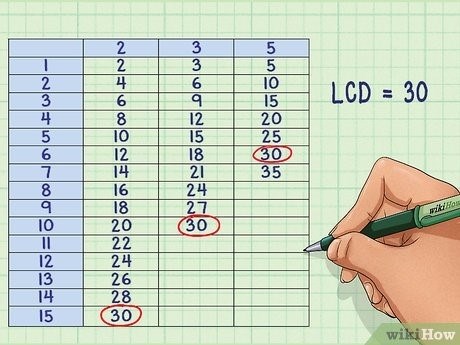
Общий знаменатель также помогает сравнить две или более дроби на основе их значения. Сравнение дробей с разными знаменателями может быть сложным, поэтому приведение к общему знаменателю позволяет сравнивать их числители напрямую.
В целом, нахождение общего знаменателя является важным шагом при работе с дробями. Он позволяет объединять, сравнивать и выполнять арифметические операции с этими числами, что облегчает решение задач и анализ данных.