В математике деление – это математическая операция, позволяющая разделить одно число на другое. Для удобства и наглядности, часто используются примеры в столбик. В данной статье рассматриваются примеры деления, представленные в виде столбикового способа, с указанием всех шагов и правил выполнения операции.
Запись чисел при делении столбиком
При записи чисел при делении столбиком следует придерживаться следующих правил:
- Делимое (число, которое делится) записывается над чертой, а делитель (число, на которое делится) записывается под чертой
- На каждом шаге вычислений, результат записывается под числом, которое делится
- Если после деления остается остаток, он записывается справа от результата и становится делимым следующего шага
Пример записи чисел при делении столбиком:
- Пусть дано деление 5678 на 23
- Записываем делимое (5678) над чертой и делитель (23) под чертой:
5678 | 23
- Получаем частное, записывая его под делимым числом:
2465678 | 23
- В случае остатка, он записывается справа от частного и становится делимым следующего шага:
2465678 | 23414
- Процесс продолжается, пока не будет достигнуто точное деление или получен остаток, который уже нельзя сократить
Запись чисел при делении столбиком помогает визуализировать процесс деления, что делает его более наглядным и понятным. При выполнении деления столбиком важно следовать указанным правилам и не допускать ошибок, чтобы получить правильный результат.
Деление столбиком на однозначное число
Основные шаги деления столбиком на однозначное число:
- Записываем делимое и делитель в столбик.
- Начинаем деление с самого старшего разряда делимого.
- Делим первую цифру делимого на делитель. Если после деления остаток равен нулю, записываем результат. Если остаток не равен нулю, записываем цифру результат и переносим остаток в следующий разряд.
- Повторяем шаг 3 для остальных цифр делимого, записывая результаты в столбик.
- Если все цифры делимого разделены, остатка не осталось. Если остался остаток, записываем его отдельно после результатов.
Пример деления столбиком на однозначное число:
| 4 | делимое |
| : | делитель |
| 3 | частное |
| , | остаток |
Например, при делении числа 158 на 4:
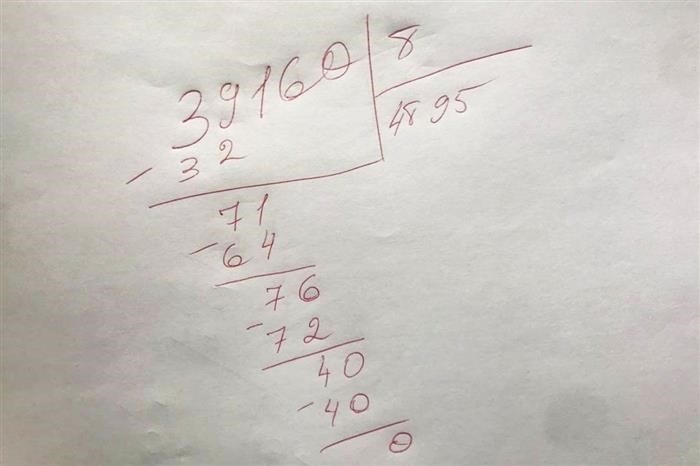
| 1 | 5 | 8 | |
| : | 4 | ||
| 3 | , | 1 |
В результате получаем, что 158 делится на 4 с частным равным 3 и остатком 1.
Деление столбиком на однозначное число позволяет упростить процесс деления и получить точный результат. Этот метод используется как в школьной математике, так и в реальных вычислениях, где требуется деление чисел на однозначное число.
Алгоритм деления столбиком
Шаги алгоритма деления столбиком:
- Записать делимое и делитель в столбик, выровняв их по правому краю.
- Взять первую цифру делимого и поделить ее на делитель. Записать результат над цифрой в столбике делителя.
- Умножить результат деления на делитель и записать полученное произведение под первым числом делимого.
- Вычесть полученное произведение из первого числа делимого и записать разность под строчкой.
- Перенести следующую цифру делимого в столбик делителя и повторить шаги с 2 по 4, пока не закончатся цифры делимого.
- Полученные результаты деления составляют цифры частного, а последнее число полученного остатка будет являться остатком от деления.
Пример:
| 1 | 8 |
| 16 | | 3 |
1. Взята первая цифра делимого (1) и заменена под строчкой делителя.
2. 1 поделено на 3 равно 0, записано в столбике над 1.
3. 0 умножено на 3 равно 0, записано под 1.
4. Разность (1 – 0) равна 1, записана под линией.
Далее повторяются шаги 2-4 для следующей цифры (6) делимого:
| 1 | 8 |
| 16 | | 3 |
| 15 |
5. Взята следующая цифра делимого (6) и подставлена под строчку делителя.
6. 16 поделено на 3 равно 5, записано в столбике над 6.
7. 5 умножено на 3 равно 15, записано под 6.
8. Разность (16 – 15) равна 1, записана под линией.
Получается, что результат деления 18 на 3 равен 5, а остаток равен 1:
18 : 3 = 5 (остаток 1)
Алгоритм деления столбиком позволяет удобно и точно вычислять результат деления чисел, оптимизируя процесс и избегая ошибок.
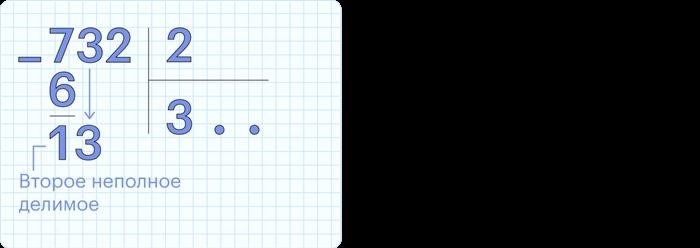
Как найти первое неполное делимое в математике
В математике существует понятие неполного делимого. Это число, которое не делится нацело на другое. Найдение первого неполного делимого может быть полезно в различных ситуациях, например, при вычислении остатка от деления или при решении задач по модулю. В этой статье будет рассмотрен метод нахождения первого неполного делимого.
Шаг 1: Выбор числа, которое будет делиться
В первую очередь нужно выбрать число, которое будет делиться на другое. Назовем его делимым числом. Обычно это число выбирают наибольшим из двух чисел, но в задачах может быть иное условие.
Шаг 2: Выбор числа, на которое будет делиться
Далее нужно выбрать число, на которое будет делиться делимое число. Назовем его делителем. Обычно это число выбирают наименьшим из двух чисел, но в задачах может быть иное условие.
Шаг 3: Деление делимого числа на делитель
Следующий шаг заключается в делении делимого числа на делитель. Если результат деления является целым числом, то это означает, что деление произошло нацело, и делимое число не является неполным делимым. Если же результат деления не является целым числом, то это означает, что делимое число является неполным делимым.
Пример
| Делимое число | Делитель | Результат деления | Остаток |
|---|---|---|---|
| 10 | 3 | 3.333… | 1 |
В данном примере число 10 является делимым, а число 3 является делителем. Результат деления равен 3.333…, что не является целым числом, поэтому делимое число 10 является первым неполным делимым.
Найдение первого неполного делимого может быть полезно при решении различных задач. В данной статье был рассмотрен метод нахождения первого неполного делимого. Запомните, что если результат деления не является целым числом, то делимое число является неполным делимым.
Умножьте делитель на полученную цифру
При выполнении деления в столбик необходимо умножить делитель на цифру, полученную в результате деления предыдущих разрядов. Данная операция позволяет получить новое значение, которое будет использоваться на следующем шаге.
Как умножить делитель на полученное число:
- Возьмите полученную цифру после деления предыдущих разрядов.
- Умножьте эту цифру на делитель.
- Запишите результат умножения под делимым в текущем разряде.
- Вычтите полученное значение из текущего разряда делимого.
- Перейдите к следующему разряду и продолжите деление в столбик.
Пример:
| Делимое | Делитель | Полученная цифра | Результат умножения |
|---|---|---|---|
| 3472 | 23 | 1 | 23 |
| -23 | |||
| -12 | |||
| 5 (остаток) |
В данном примере мы умножили делитель 23 на полученную цифру 1 и записали результат 23. Затем вычли это значение из первого разряда делимого. Продолжая процесс деления в столбик, мы получили результат 152 с остатком 5.
Таким образом, умножение делителя на полученную цифру является одной из ключевых операций при выполнении деления в столбик. Это позволяет получить верный результат и осуществить продолжение процесса деления.
Как делить числа с остатком?
Для более эффективного понимания и освоения данного математического процесса, следует рассмотреть несколько основных шагов и методов, которые помогут в делении чисел с остатком.
Шаг 1: Разделение чисел
Первый шаг – это разделение чисел. Убедитесь, что у вас есть два числа – делимое и делитель. Делимое – это число, которое надо разделить, а делитель – это число, на которое нужно разделить делимое. Например, если у вас есть число 15, которое вы хотите разделить на число 4, то 15 – это делимое, а 4 – это делитель.

Для выполнения деления используйте обычную математическую операцию деления: делимое / делитель.
Шаг 2: Нахождение частного
Второй шаг – найти частное. Частное – это результат деления чисел. В нашем примере с числами 15 и 4, частным будет 3 (15 / 4 = 3).
Шаг 3: Определение остатка
Третий шаг – это определение остатка. Остаток – это число, которое остается после выполнения деления чисел. Для его нахождения необходимо понять, сколько раз делитель полностью помещается в делимое и какое количество остается.
| Делимое | Делитель | Частное | Остаток |
|---|---|---|---|
| 15 | 4 | 3 | 3 |
В нашем примере 15 / 4 = 3 с остатком 3. Это означает, что после трех полных делений в результате остаются еще 3 единицы, которые не могут быть разделены на делитель.
Шаг 4: Запись результата
Четвертый и последний шаг – запись результата деления. Результат деления чисел с остатком можно записать в виде десятичной дроби, где частное – это целая часть, а остаток – это дробная часть.
В нашем случае результат будет записываться как 3+3/4.
Примеры деления чисел с остатком:
- 17 / 5 = 3+2/5
- 23 / 6 = 3+5/6
- 14 / 3 = 4+2/3
Таким образом, деление чисел с остатком требует разделения чисел, нахождения частного и определения остатка. Результат деления можно записать в виде десятичной дроби, где частное – это целая часть, а остаток – это дробная часть.
Определите, сколько будет цифр в частном
При выполнении деления одного числа на другое возникает вопрос о количестве цифр в частном. Для определения этого количества можно использовать несколько простых правил и формул.
Правило 1: Знаки чисел влияют на количество цифр
Если делимое и делитель имеют одинаковую четность или нечетность, то в частном будет на одну цифру больше, чем в делимом.
Например, если делимое имеет 3 цифры и делитель – 2 цифры, то количество цифр в частном будет равно 4.
Правило 2: Знаки чисел не влияют на количество цифр
Если делимое и делитель имеют разную четность или нечетность, то количество цифр в частном будет такое же, как в делимом.
Например, если делимое имеет 4 цифры и делитель – 3 цифры, то количество цифр в частном также будет равно 4.
Формула: Количество цифр в частном
Общую формулу, позволяющую определить количество цифр в частном, можно записать следующим образом:
Количество цифр в частном = количество цифр в делимом – количество цифр в делителе + 1
Примеры:
- Делимое: 123456, делитель: 12
Количество цифр в частном = 6 – 2 + 1 = 5 - Делимое: 987654321, делитель: 123
Количество цифр в частном = 9 – 3 + 1 = 7 - Делимое: 1000, делитель: 10
Количество цифр в частном = 4 – 2 + 1 = 3
Таблица “Количество цифр в частном”
| Делимое | Делитель | Количество цифр в частном |
|---|---|---|
| 123456 | 12 | 5 |
| 987654321 | 123 | 7 |
| 1000 | 10 | 3 |
Как делить однозначные и многозначные числа в столбик с остатком
Шаг 1: Расстановка чисел
В начале необходимо расставить числа в правильном порядке. Делимое располагается над делителем, начиная с самой левой цифры. Если число многозначное, сначала делится первая цифра, затем вторая и так далее.
Шаг 2: Проверка
Необходимо проверить, можно ли поделить первую цифру делимого на делитель. Если можно, то записываем частное над делителем, если нет, то записываем ноль.
Шаг 3: Вычитание
Если частное записано, то необходимо умножить делитель на частное и вычесть полученный результат из делимого. Записываем результат вычитания под строчкой.
Шаг 4: Перенос цифры
Переносим следующую цифру из делимого к полученному результату и повторяем шаги 2 и 3 до тех пор, пока не закончатся цифры в делимом числе.
Шаг 5: Запись ответа
Когда все цифры делимого обработаны, записываем полученные частное и остаток. Частное будет являться ответом, а остаток – остатком от деления.
В таблице ниже представлен пример деления 2354 на 19:
| Делимое | Делитель | Частное | Остаток |
|---|---|---|---|
| 2 | 19 | 0 | 2 |
| 23 | 19 | 1 | 4 |
| 235 | 19 | 12 | 7 |
| 2354 | 19 | 123 | 13 |
Таким образом, результат деления 2354 на 19 равен 123 с остатком 13.
Вычтите это число из неполного делимого
Если вы хотите вычесть число из неполного делителя, следуйте этим простым шагам:
- Запишите неполное делимое и число, которое вы хотите вычесть, одно под другим.
- Разместите цифры в одной колонке по правилам вычитания, начиная с правого столбца.
- Вычтите каждую цифру в столбике, начиная с крайнего правого столбца. Запишите результат вычитания под соответствующей цифрой в столбце разности.
- Если в столбце уменьшаемых цифр закончились, а в столбце вычитаемых цифр они еще остались, просто приставьте оставшиеся цифры к соответствующим цифрам в разности.
Например, если у нас есть неполное делимое 437 и мы хотим вычесть из него число 123, мы можем выполнить следующие шаги:
| Столбец неполного делимого | Столбец числа для вычитания | Столбец разности |
| 4 | 1 | 3 |
| 3 | 2 | 1 |
| 7 | 3 | 4 |
В результате, результатом операции будет 314.
Вычитание числа из неполного делимого является простой арифметической операцией, которая помогает нам решать различные математические задачи. Пользуйтесь этой техникой в своих расчетах и задачах для получения точного результата.
Деление многозначных натуральных чисел столбиком
Шаги деления столбиком:
- Поделить первую цифру делимого числа на делитель.
- Умножить результат деления на делитель и вычесть полученное произведение из первой цифры делимого числа.
- Записать полученный результат под первой цифрой числа и приступить к следующей цифре.
- Получить следующую цифру делимого числа и добавить ее к оставшимся цифрам слева.
- Повторять шаги 1-4 до тех пор, пока не будет получен остаток 0 или пока не будут исчерпаны все цифры делимого числа.
Пример деления столбиком:
| 587 | : | 7 | = | 83 |
На первом шаге мы делим цифру 5 на 7 и получаем результат 0. Результат записываем под цифрой 5.

| 587 | : | 7 | = | 83 |
| 0 |
На следующем шаге мы умножаем результат деления (0) на делитель (7) и вычитаем полученное произведение (0) из первой цифры делимого числа (5). Получаем остаток 5 и записываем его слева от следующей цифры числа.
| 587 | : | 7 | = | 83 |
| 0 | ||||
| 5 |
Затем мы получаем следующую цифру делимого числа (8) и добавляем ее к остатку (5) слева. Получаем число 58 и делим его на делитель (7).
| 587 | : | 7 | = | 83 |
| 0 | ||||
| 5 | ||||
| 58 |
Повторяем шаги деления до тех пор, пока не достигнем остатка 0. Получаем результат деления – 83.
Деление столбиком является эффективным методом для деления многозначных чисел. Он позволяет получить точный результат и упростить процесс деления. Метод столбиком особенно полезен, когда необходимо делить большие числа или когда требуется высокая точность в результатах деления.
Деление с остатком: основные принципы и примеры
Принцип деления с остатком заключается в том, что при делении одного числа (называемого делимым) на другое число (называемое делителем), получается какое-то количество целых частей и остаток, который остается после деления.
Примеры деления с остатком:
-
Делимое: 15
Делитель: 4
Результат деления: 3
Остаток: 3
15 = 4 * 3 + 3
-
Делимое: 27
Делитель: 5
Результат деления: 5
Остаток: 2
27 = 5 * 5 + 2
-
Делимое: 100
Делитель: 7
Результат деления: 14
Остаток: 2
100 = 7 * 14 + 2
Как видно из примеров, результат деления представляет собой наибольшее целое число, которое не превышает результат деления, а остаток представляет собой разницу между делимым и произведением делителя на результат деления.
Применение деления с остатком:
- Определение четности или нечетности чисел
- Нахождение остатка от деления в алгоритмах и программировании
- Вычисление степеней чисел
- Проверка делимости чисел
- Расчет времени и даты
- Описание рациональных чисел
Деление с остатком является фундаментальным математическим понятием, которое имеет широкий спектр применений и важно для понимания многих других математических и алгоритмических концепций.
Правила деления для детей: пошаговая инструкция с примерами и объяснениями
Правило 1: Деление – это обратная операция умножению
Деление – это противоположная операция умножению. Если мы знаем результат умножения двух чисел, мы можем найти один из множителей, используя деление. Например, если у нас есть число 12 и знание, что оно получено путем умножения на 3, мы можем найти значение множителя, разделив 12 на 3.
Правило 2: Значение деления – это результат
Результат деления двух чисел называется частным. Частное – это число, которое мы получаем в результате деления. Оно показывает, сколько раз одно число умещается в другое число. Например, если мы делим число 10 на число 2, мы получаем частное равное 5. Это означает, что число 2 умещается в число 10 пять раз.
Правило 3: Значение делителя влияет на результат деления
Значение делителя – это число, на которое мы делим другое число. Если значение делителя больше единицы, частное будет меньше делимого числа. Например, если мы делим число 9 на 3, мы получаем частное равное 3. В этом случае, значение делителя 3 делит число 9 на три равные части.
Правило 4: Остаток может быть результатом деления
Остаток – это число, которое остается после выполнения деления. Иногда, когда число не делится нацело, мы получаем остаток. Например, если мы делим число 5 на 2, мы получаем частное равное 2 и остаток равный 1. Это означает, что число 5 делится на 2 два раза с остатком 1. Остаток является частью числа, которую мы не можем разделить поровну.
Практические примеры деления
- Пример 1: 12 ÷ 3 = 4
- Здесь мы делим число 12 на значение делителя 3.
- Частное равно 4, потому что число 12 умещается в число 3 четыре раза.
- Этот пример не имеет остатка, потому что число 12 делится на число 3 без остатка.
- Пример 2: 10 ÷ 2 = 5
- Здесь мы делим число 10 на значение делителя 2.
- Частное равно 5, потому что число 10 умещается в число 2 пять раз.
- Этот пример не имеет остатка, потому что число 10 делится на число 2 без остатка.
- Пример 3: 9 ÷ 3 = 3 (остаток 0)
- Здесь мы делим число 9 на значение делителя 3.
- Частное равно 3, потому что число 9 умещается в число 3 три раза.
- Этот пример не имеет остатка, потому что число 9 делится на число 3 без остатка.
- Пример 4: 5 ÷ 2 = 2 (остаток 1)
- Здесь мы делим число 5 на значение делителя 2.
- Частное равно 2, потому что число 5 умещается в число 2 два раза.
- Остаток равен 1, потому что после деления числа 5 на число 2 остается одна неразделенная часть.
Правила деления помогут ребёнку понять, как разделить числа. Пошаговая инструкция и примеры помогут закрепить знания и позволят применить их на практике.
Примеры на деление уголком для начальной школы
Пример 1:
Разделим число 45 на 3 уголка:
- Начнем с единицы, разделим 4 на 3 – получим 1. Пропишем результат на верхней части уголка.
- Умножим полученное число (1) на делитель (3) и вычтем результат (3) из делимого (4) – получим остаток 1.
- Продолжим деление, прописывая полученные результаты и остатки на верхней части уголка. Результат – 15.
- Остаток (1) станет первой цифрой следующего разряда.
- Умножим остаток (1) на делитель (3) и вычтем результат (3) из делимого (5) – получим остаток 2.
- Закончим деление, записав полученные результаты и остатки.
Результат деления числа 45 на 3 уголком: 15, остаток 2.
Пример 2:
Разделим число 72 на 9 уголков:
- Начнем с единицы, разделим 7 на 9 – получим 0. Пропишем результат на верхней части уголка.
- Умножим полученное число (0) на делитель (9) и вычтем результат (0) из делимого (7) – получим остаток 7.
- Продолжим деление, прописывая полученные результаты и остатки на верхней части уголка. Результат – 0.
- Остаток (7) станет первой цифрой следующего разряда.
- Умножим остаток (7) на делитель (9) и вычтем результат (63) из делимого (72) – получим остаток 9.
- Закончим деление, записав полученные результаты и остатки.
Результат деления числа 72 на 9 уголком: 8, остаток 9.
Деление дробей в столбик: примеры и правила
Основные правила деления дробей в столбик:
- Записывается делимое и делитель в виде десятичной дроби.
- Если целая часть делимого отсутствует, ставится ноль и деление производится с действительными числами.
- Переводим делитель из десятичной в обыкновенную дробь.
- Умножаем делимое и делитель на числа таким образом, чтобы делитель стал целым числом.
- Решаем деление как обычную задачу на деление целых чисел.
- Если в делимом или делителе присутствует остаток, оставляем его и продолжаем деление.
- Выражаем результат деления в виде десятичной дроби или сокращенной обыкновенной дроби.
Пример деления дробей в столбик:
| Делимое: | 1/2 |
| Делитель: | 1/4 |
Переведем дробь 1/4 в целое значение, домножив числитель и знаменатель на 4:
| Делимое: | 1/2 |
| Делитель: | 4/1 |
Теперь можно провести деление:
1/2 ÷ 4/1 = 1/2 × 1/4 = 1/8
Итак, результат деления дробей 1/2 и 1/4 равен 1/8.
В случае, если делимое или делитель имеют остаток, следует продолжать деление до получения точного результата.
Деление дробей в столбик является важным математическим навыком, который позволяет решать различные задачи, связанные с дробными значениями. Правильное применение правил деления дробей в столбик позволяет получить точный результат и упрощенную форму дроби.
Запишите делимое и делитель с уголком
Для записи делимого и делителя с использованием уголка, можно воспользоваться следующими принципами:
- Поместите делимое под делителем, сокращая пробелы между цифрами, если это необходимо.
- Поместите уголок после последней цифры делимого и перед первой цифрой делителя.
- При записи многоразрядных чисел, убедитесь, что цифры делимого и делителя находятся под соответствующими разрядами.
Примеры:
| Делимое: | Делитель: | Запись: |
| 25 | 5 | 25 ÷ 5 |
| 135 | 9 | 135 ÷ 9 |
| 876 | 12 | 876 ÷ 12 |
| 4500 | 30 | 4500 ÷ 30 |
Корректная запись делимого и делителя с использованием уголка помогает четко определить параметры деления и упрощает понимание математического выражения. Будьте внимательны при записи числовых значений и следуйте указанным принципам для достижения правильного результата.
Делим в столбик правильно
Шаг 1. Подготовка
Перед тем как приступить к делению, необходимо выполнить несколько подготовительных шагов:
- Разделить делимое число на делитель, записывая результат в “стать” под делимым числом.
- Если деление не является целым, то добавить ноль после делимого числа и продолжить деление.
- Разделить остаток от предыдущего деления на делитель и записать результат под результатом предыдущего деления.
Шаг 2. Выполнение деления
Теперь можно приступить к самому делению:
- Взять первую цифру делимого числа и записать ее над знаком деления.
- Определить наибольшее число, на которое можно умножить делитель и получить результат, не превышающий цифру, записанную над знаком деления. Записать это число под делимым числом и вычислить произведение.
- Вычесть полученное произведение из делимого числа и записать разность под ним.
- Опустить следующую цифру делимого числа и дописать ее к последней разности.
- Повторить шаги 2-4, пока делимое число не будет полностью потрачено.
Шаг 3. Запись результата
После того, как все цифры делимого числа будут потрачены, можно записать результат:
- Под последней разностью записать остаток, если он есть. В противном случае, остаток равен нулю.
- Составить частное, записывая по цифре под цифрой результаты деления.
Таким образом, следуя этим простым правилам, можно правильно выполнить деление в столбик и получить верный результат расчета.
Распределите финансовую нагрузку с картой «Халва»
В статье мы рассмотрели карту «Халва», которая поможет вам упростить распределение финансовой нагрузки между участниками групповых проектов или совместных покупок. Это удобное и надежное решение для тех, кто хочет избежать лишних хлопот и конфликтов при оплате общих расходов.
Мы рассмотрели основные преимущества карты «Халва»:
- Возможность создания групповых счетов, на которые поступает финансирование от участников группы.
- Автоматическое распределение платежей между участниками проекта или покупки.
- Отчетность о расходах и платежах каждого участника.
- Удобство и простота использования.
Теперь вы можете забыть о неудобствах и непонимании, кто кому сколько должен. Карта «Халва» позволяет справляться с финансовыми задачами в группе быстро и без лишних хлопот. Распределите финансовую нагрузку с помощью «Халва» и наслаждайтесь процессом работы или отдыха вместе!