Сложение и вычитание чисел с разными знаками – основные операции в математике, которые позволяют получить результат, учитывая знаки чисел. При сложении двух чисел с одним знаком, их значения складываются, а знак остается таким же. Если у чисел разные знаки, то выполняется вычитание по абсолютным значениям чисел, а знак результата определяется знаком числа с большим абсолютным значением. Эти операции широко используются в повседневной жизни и в различных областях науки и техники.
Порядок выполнения действий с числами
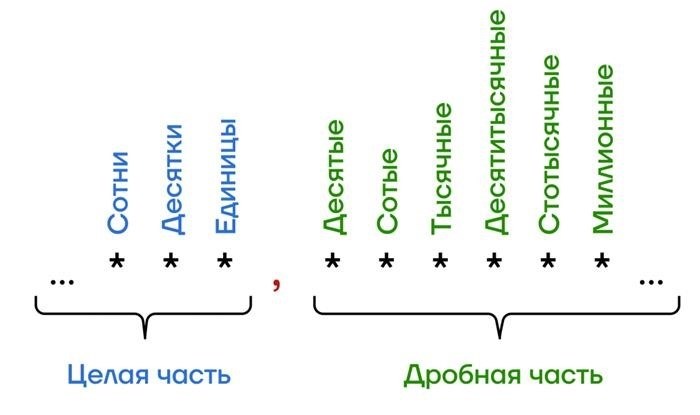
Сложение чисел с разными знаками
Если слагаемые имеют разные знаки, то вычитание выполняется по следующему правилу: нужно вычесть модуль числа со знаком от модуля числа с противоположным знаком и присвоить результат числу с тем знаком, которым обладает число с большим модулем.
Например:
- 7 + (-5) = 2 (здесь 5 больше, чем 7, поэтому результат имеет знак “минус”)
- 9 + (-12) = -3 (здесь 12 больше, чем 9, поэтому результат имеет знак “минус”)
- -4 + 6 = 2 (здесь 6 больше, чем 4, поэтому результат имеет знак “плюс”)
Вычитание чисел с разными знаками
При вычитании чисел с разными знаками, вычитание выполняется по правилам сложения, но со знаком противоположным знаку вычитаемого числа.

Например:
- 5 – (-3) = 8 (знак у отрицательного числа меняется на противоположный, результат имеет знак “плюс”)
- -7 – (-2) = -5 (знак у отрицательного числа меняется на противоположный, результат имеет знак “минус”)
- 2 – (-8) = 10 (знак у отрицательного числа меняется на противоположный, результат имеет знак “плюс”)
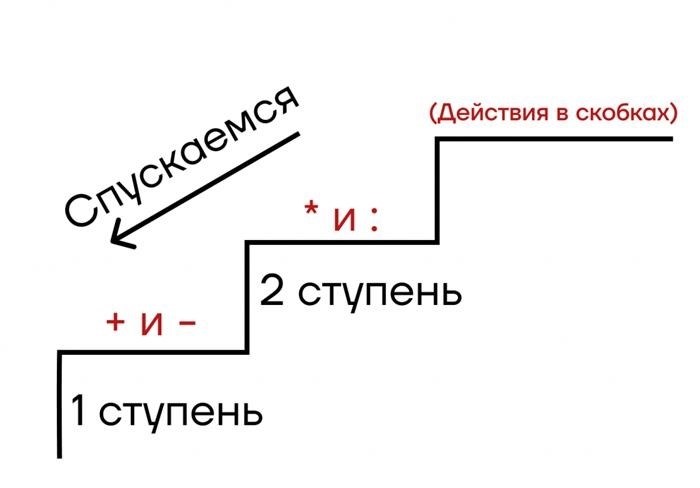
Порядок выполнения действий (знаменатель должен быть в скобках)
При выполнении действий в одном выражении с числами, сначала выполняются действия в скобках, затем умножение и деление, а после сложение и вычитание.
Например:
- 2 + (3 * 4) = 14 (сначала выполняется умножение, затем сложение)
- 6 – (2 + 3) = 1 (сначала выполняется сложение в скобках, затем вычитание)
- (4 + 5) * 2 = 18 (сначала выполняется сложение в скобках, затем умножение)
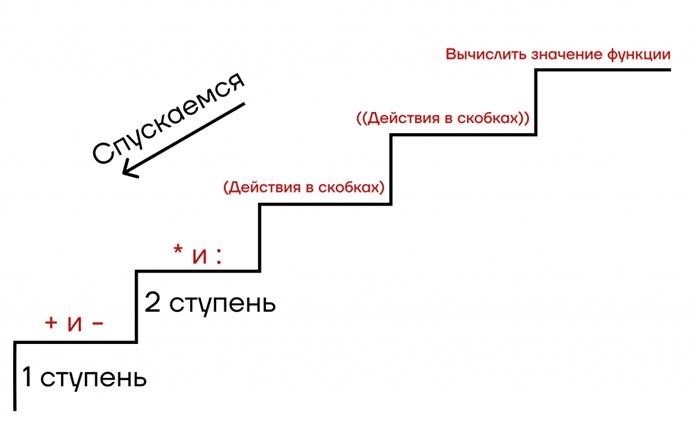
Порядок выполнения операций в выражениях (это просто по поряеку)
- Выполняются действия в скобках.
- Выполняются умножение и деление слева направо.
- Выполняются сложение и вычитание слева направо.
Правильное понимание порядка выполнения действий с числами помогает в решении математических задач и облегчает работу с числами. Соблюдение данных правил поможет избежать ошибок и сделать вычисления точными и своевременными.
Примеры упражнений на вычитание
Упражнение 1: Вычитание положительного числа из отрицательного числа
Дано: -7 – 3 = ?
Решение: для выполнения данной операции необходимо сначала изменить знак числа, из которого вычитают. Затем складываем результаты чисел и сохраняем общий знак, получая окончательный ответ: -7 – 3 = -10.
Упражнение 2: Вычитание отрицательного числа из положительного числа
Дано: 9 – (-5) = ?
Решение: для выполнения данной операции необходимо изменить знак числа, которое вычитают, на противоположный. Затем складываем числа и сохраняем общий знак, получая окончательный ответ: 9 – (-5) = 14.
Упражнение 3: Вычитание положительного числа из положительного числа
Дано: 15 – 7 = ?
Решение: в данной операции оба числа являются положительными. Просто вычитаем число из другого, сохраняя знак операции: 15 – 7 = 8.
Упражнение 4: Вычитание отрицательного числа из отрицательного числа
Дано: -12 – (-4) = ?
Решение: в данной операции оба числа являются отрицательными. Изменяем знак числа, которое вычитают, и складываем числа, сохраняя знак операции: -12 – (-4) = -8.
Упражнение 5: Составные операции на вычитание чисел с разными знаками
Дано: 8 – (-3) + (-6) – 12
Решение: в данной составной операции выполняем вычитание чисел последовательно. Изменяем знак числа, которое вычитают, и складываем числа, сохраняя знак операции. Поэтапно решаем каждую часть: 8 – (-3) = 11, 11 + (-6) = 5, 5 – 12 = -7. Ответ: 8 – (-3) + (-6) – 12 = -7.
Как правильно выполнять вычитание
1. Получение разности
Для выполнения вычитания следует следующая последовательность действий:
- Поставьте вычитаемое число под вычитающим так, чтобы разряды чисел были согласованы вертикально.
- Начиная с самого правого разряда, выполните вычитание цифр этой позиции. Если разряд вычитаемого числа меньше разряда вычитающего числа, возможно понадобится проведение заема.
- При проведении заема из следующего разряда, уменьшите его на единицу.
- Продолжайте вычитание по каждому разряду чисел, проводя заемы при необходимости.
- Результат будет числом с противоположным знаком от заемаемого числа, если оно было больше вычитающего, или с тем же знаком, если разность отрицательная.
2. Работа с отрицательными числами
Вычитание отрицательных чисел требует особого внимания. При вычитании отрицательного числа у нас получается сложение, где знаки одинаковы, а при вычитании из отрицательного числа, знаки отличаются.
Пример:
| Вычитающее | Число | Разность |
| 5 | -3 | 5 + (-3) = 2 |
| -2 | -7 | -2 – (-7) = -2 + 7 = 5 |
3. Примеры вычитания
Для наглядности рассмотрим несколько примеров вычитания:
- Пример 1: 67 – 23 = 44
- Пример 2: -42 – 15 = -57
- Пример 3: -32 – (-17) = -32 + 17 = -15
- Пример 4: 78 – (-43) = 78 + 43 = 121
Помните, что для успешного выполнения вычитания необходимо внимательно следить за знаками чисел, правильно согласовывать разряды и проводить заемы при необходимости. Практикуйтесь на различных примерах, чтобы научиться выполнять вычитание легко и безошибочно.
Действия с числами разных знаков: Подведение итога
В этой статье мы рассмотрели основные операции сложения и вычитания чисел с разными знаками. Данные действия возникают при работе с числами, которым присвоены положительные и отрицательные значения.

Когда мы складываем два числа с разными знаками, результат может быть положительным или отрицательным в зависимости от величины чисел и их знаков. Если слагаемые числа имеют противоположные знаки, мы вычитаем из большего числа по модулю меньшее число и приписываем знак числу с большим по модулю значением. Если же слагаемые числа имеют одинаковые знаки, мы складываем их по модулю и приписываем результату этот же знак.
Вычитание чисел с противоположными знаками можно свести к сложению, меняя знаки слагаемых чисел и выполняя сложение. Таким образом, действия с числами разных знаков довольно просты и интуитивно понятны.
Важно помнить, что при выполнении этих действий нужно учитывать знаки чисел и правильно определять результат. Использование математических правил и понимание сути операций помогут успешно выполнять сложение и вычитание чисел с разными знаками. В специальных случаях, например при работе с отрицательными координатами или финансовыми данными, знание и понимание операций с числами разных знаков может быть особенно полезным.