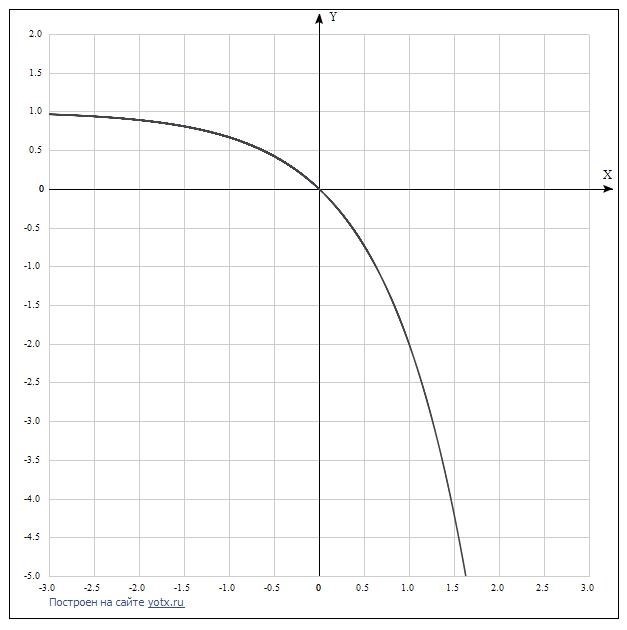
Показательная функция является одной из важных математических функций, которая используется во многих областях науки и техники. Ее график имеет особенности, которые отражают ее свойства и позволяют проводить различные анализы и вычисления. Показательная функция хорошо изучена и имеет ряд полезных свойств, которые помогают решать множество задач и задавать функциональные зависимости.
Применение показательных функций в реальной жизни
1. Экономика и финансы
В экономике и финансах показательные функции используются для оценки и прогнозирования различных макроэкономических и финансовых показателей. Например, они могут быть применены для анализа инфляции, уровня безработицы, роста ВВП, курса валют, доходности инвестиций и других финансовых показателей.
Показательные функции также могут использоваться для определения эффективности компаний и организаций. Например, с их помощью можно проанализировать прибыльность предприятия, долю рынка, уровень ликвидности, долговую нагрузку и другие показатели, которые влияют на финансовое состояние организации.
2. Наука и исследования
В научных исследованиях показательные функции используются для анализа и интерпретации данных, полученных в ходе экспериментов. Они позволяют выявить закономерности, установить взаимосвязи между различными переменными и определить степень влияния факторов на исследуемые явления.
3. Спорт и физическая активность
Показательные функции находят применение в анализе спортивных результатов и физической активности. Они помогают спортсменам и тренерам определить эффективность тренировочных программ, прогнозировать достижение спортивных результатов и разрабатывать стратегии достижения спортивных целей.
С помощью показательных функций можно анализировать данные о времени, скорости, мощности и личных рекордах спортсменов. Например, они могут быть использованы для определения оптимального темпа бега на длительные дистанции, оптимальной нагрузки при тренировках, оценки силовых показателей при подъеме весов и других аспектов спортивной деятельности.
Применение показательных функций в реальной жизни является важным инструментом для анализа данных, прогнозирования результатов и принятия решений. Они находят применение в экономике, науке, спорте и других областях деятельности, где требуется структурирование и интерпретация данных. Умение использовать показательные функции позволяет получить более точные и надежные результаты в различных сферах жизни.
Логарифмическая функция
Логарифмическая функция определяется как обратная функция к экспоненциальной функции. То есть, если y = b x является экспоненциальной функцией, то x = logby является логарифмической функцией.
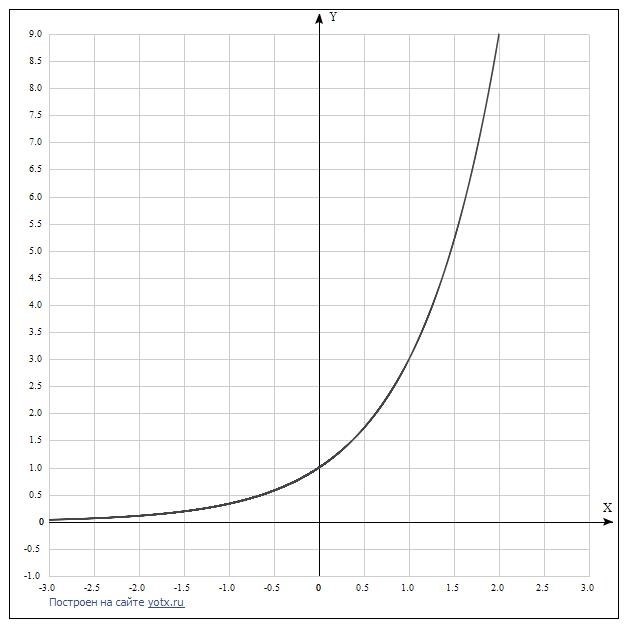
Основные свойства логарифмической функции:
- Логарифмическая функция определена только для положительных значений аргумента.
- Базис логарифма определяет, какому числу соответствует единичный логарифм. Например, в случае натурального логарифма (базис равен числу Эйлера e), если ln(x) = y, то x = e y.
- Один из наиболее известных базисов логарифмической функции – десятичный логарифм, обозначаемый как log(x) или log10(x). Таким образом, если log(x) = y, то x = 10 y.
- Логарифм от произведения двух чисел равен сумме логарифмов этих чисел: ln(xy) = ln(x) + ln(y). Это свойство называется свойством произведения.
- Логарифм от степени числа равен произведению степени логарифма: ln(x a) = a * ln(x). Это свойство называется свойством степени.
Применение логарифмической функции:
Логарифмическая функция имеет широкое применение в различных областях. Например, в физике она применяется для моделирования процессов, где изменение величин происходит согласно определенным логарифмическим законам. В экономике логарифмическая функция используется для изучения процентного роста и децентного спада. В биологии она может быть использована для анализа роста популяций и др.
Таким образом, логарифмическая функция является важным инструментом в математике и имеет широкое применение в различных областях. Знание этой функции позволяет углубиться в понимание сложных процессов и явлений и эффективно их анализировать.