Логарифмическая функция – это математическая функция, обратная к экспоненциальной функции. График логарифмической функции имеет форму увеличивающейся кривой, которая стремится к асимптоте. Логарифмическая функция обладает несколькими важными свойствами, такими как связь с показательной функцией, правила логарифмирования и возможность применения в различных областях науки.
Примеры исследования и построения логарифмических функций
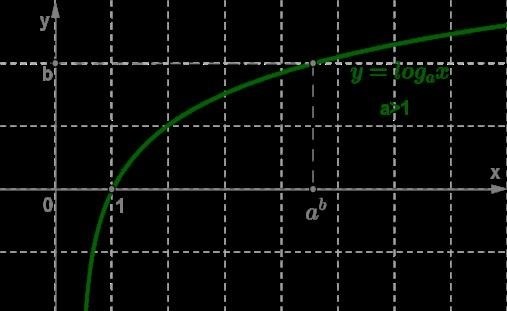
Пример 1: Построение графика логарифмической функции вида y = logₐ(x)
Для начала, рассмотрим логарифмическую функцию вида y = logₐ(x), где a – положительное число, отличное от 1. Чтобы построить график такой функции, мы можем использовать следующие шаги:
- Выберите значениев основании a. Например, a может быть равно 2, 10 или любому другому положительному числу, отличному от 1.
- Задайте значения x. Например, можно выбрать значения от 1 до 10 для создания гладкого графика.
- Вычислите значения y, используя формулу y = logₐ(x).
- Постройте точки с координатами (x, y) на графике.
- Соедините точки прямыми линиями для получения графика логарифмической функции.
Ниже приведен пример графика функции y = log₂(x). Мы выбрали значения x от 1 до 10 и вычислили соответствующие значения y.
| x | y = log₂(x) |
| 1 | 0 |
| 2 | 1 |
| 3 | 1.58496 |
| 4 | 2 |
| 5 | 2.32193 |
| 6 | 2.58496 |
| 7 | 2.80735 |
| 8 | 3 |
| 9 | 3.16993 |
| 10 | 3.32193 |
Пример 2: Исследование свойств логарифмической функции
Исследование свойств логарифмической функции может помочь нам понять ее поведение и применение в реальных уравнениях и задачах. Рассмотрим логарифмическую функцию y = logₐ(x) и рассмотрим следующие свойства:
- Область определения: Для функции y = logₐ(x) область определения состоит из положительных значений x. Например, при a = 2, функция определена для x > 0.
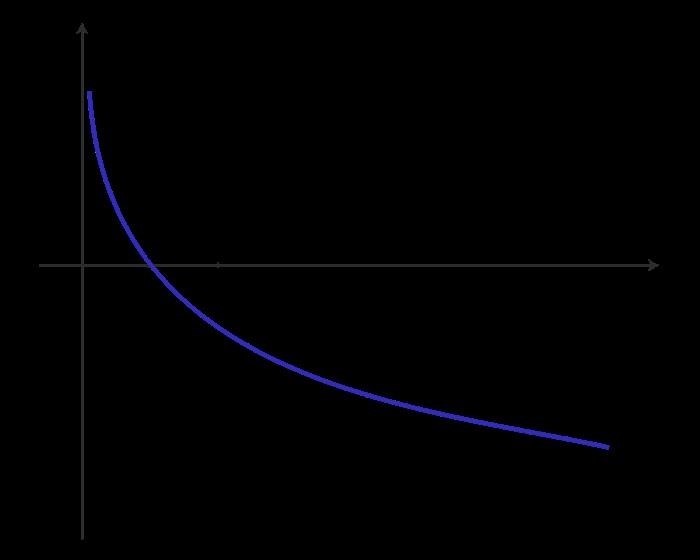
- Область значений: Область значений функции y = logₐ(x) зависит от выбранного основания a. Если a > 1, то функция имеет область значений (-∞, +∞). Если 0 < a < 1, то функция имеет область значений (-∞, 0).
- Монотонность: Функция y = logₐ(x) монотонно возрастает при a > 1 и монотонно убывает при 0 < a < 1.
- Асимптоты: У логарифмической функции y = logₐ(x) есть вертикальная асимптота в точке x = 0. Она также может иметь горизонтальную асимптоту в y = 0, если a > 1.
- Пересечение с осями: Логарифмическая функция y = logₐ(x) пересекает ось x в точке (1, 0) и ось y в точке (0, -∞).
Изучение этих свойств может помочь нам лучше понять поведение логарифмических функций и использовать их в различных математических задачах.
Основные свойства логарифмов
1. Свойство логарифма от произведения
Логарифм произведения равен сумме логарифмов.
Если даны два положительных числа a и b, то логарифм их произведения равен сумме логарифмов самих чисел:
logb(a * b) = logb(a) + logb(b)
2. Свойство логарифма от частного
Логарифм частного равен разности логарифмов.
Если даны два положительных числа a и b, то логарифм их частного равен разности логарифмов самих чисел:
logb(a / b) = logb(a) – logb(b)
3. Свойство логарифма от степени
Логарифм числа в степени равен произведению степени и логарифма числа.
Если дано положительное число a и действительное число n, то логарифм числа a в степени n равен произведению степени и логарифма числа:
logb(an) = n * logb(a)
4. Свойство логарифма от основания
Логарифм числа по основанию, равное этому числу, равен 1.
Логарифм числа по основанию, равное самому числу, всегда равен 1:
logb(b) = 1
5. Свойство логарифма от числа 1
Логарифм числа 1 по любому основанию равен 0.
Логарифм числа 1 по любому основанию всегда равен 0:
logb(1) = 0
6. Свойство логарифма от отрицательного числа
Логарифм отрицательного числа не определен.
Логарифм отрицательного числа не определен, так как логарифм берется только от положительных чисел:
logb(-a) = undefined
7. Свойство логарифма от нуля
Логарифм нуля не определен.
Логарифм нуля не определен, так как не существует числа, возведенного в какую-либо степень, равную нулю:
logb(0) = undefined
Знание основных свойств логарифмов поможет вам в решении различных математических задач и упростит вашу работу с логарифмическими функциями.
Понятие логарифма
Логарифмы широко применяются в физике, экономике, технике и других областях науки. Они позволяют сократить сложные математические операции и упростить вычисления.
Основные свойства логарифма:
- Логарифм произведения равен сумме логарифмов: loga(b*c) = loga(b) + loga(c).
- Логарифм частного равен разности логарифмов: loga(b/c) = loga(b) – loga(c).
- Логарифм степени равен произведению степеней: loga(bn) = n*loga(b).
- Логарифм от единицы по любому основанию равен нулю: loga(1) = 0.
- Логарифм от основания по самому себе равен единице: loga(a) = 1.
Примеры использования логарифма:
| a | x | b | loga(b) |
|---|---|---|---|
| 10 | 3 | 1000 | 3 |
| 2 | 8 | 256 | 4 |
| 5 | 2 | 25 | 1 |
Цитата:
“Логарифмы – мощный инструмент математики, позволяющий решать сложные задачи более простым и эффективным способом.”
Понятие логарифмической функции
Формула и свойства логарифмической функции
Логарифмическая функция может быть представлена следующей формулой:
y = logb(x)
Где:
- x – аргумент функции;
- b – основание логарифма;
- y – значение функции.
Основные свойства логарифмической функции:
- Смена основания: логарифмы с разными основаниями могут быть приведены друг к другу с помощью формулы: logb(a) = logc(a) / logc(b).
- Свойство единицы: logb(b) = 1.
- Свойство нуля: logb(0) = -бесконечность.
- Свойство произведения: logb(a * c) = logb(a) + logb(c).
- Свойство частного: logb(a / c) = logb(a) – logb(c).
График логарифмической функции
График логарифмической функции выглядит следующим образом:
| Основание б | График |
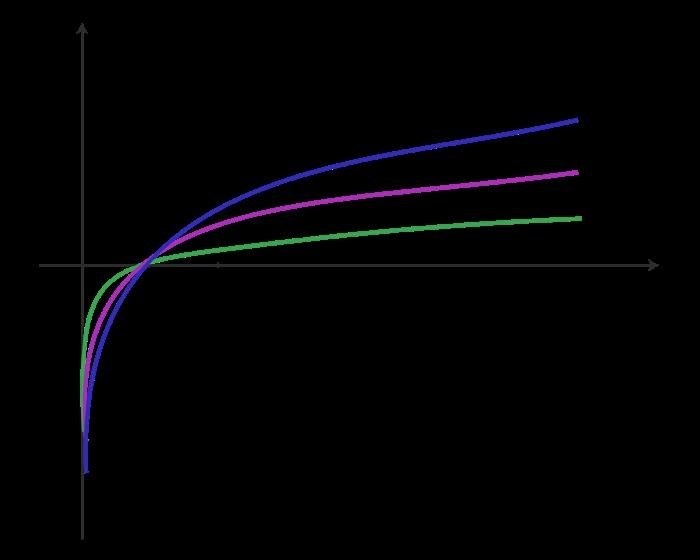
| b > 1 |  |
| b = 1 |  |
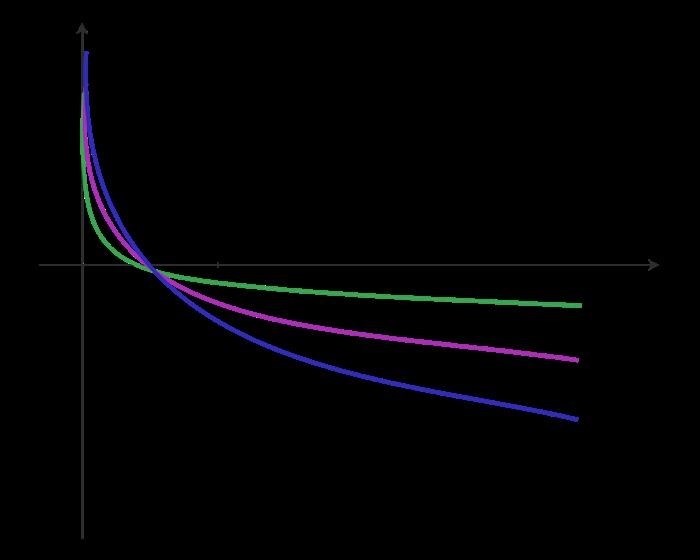
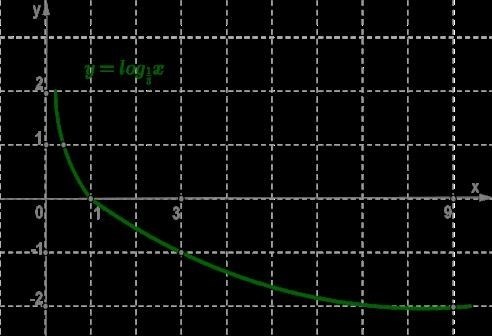
| 0 < b < 1 |  |
Вид графика логарифмической функции зависит от основания b. При b > 1 график функции возрастает. При b = 1 график является постоянной прямой. При 0 < b < 1 график убывает.
Логарифмическая функция имеет множество приложений в различных областях науки и техники. Она позволяет обработать данные и решить сложные математические задачи. Понимание основных свойств и графика логарифмической функции является важным для успешного решения задач, связанных с этим типом функций.
Подписи к слайдам:
Мы изучили, как строить график логарифмической функции, как определить область определения и область значений функции. Также мы узнали о важных свойствах логарифмических функций, таких как свойства умножения, деления, возведения в степень и корня.
Логарифмическая функция является важным инструментом в математике и науке, она широко применяется в различных областях, например, в физике, экономике и информатике. Понимание ее свойств и графика поможет вам лучше понять и анализировать различные явления и процессы.