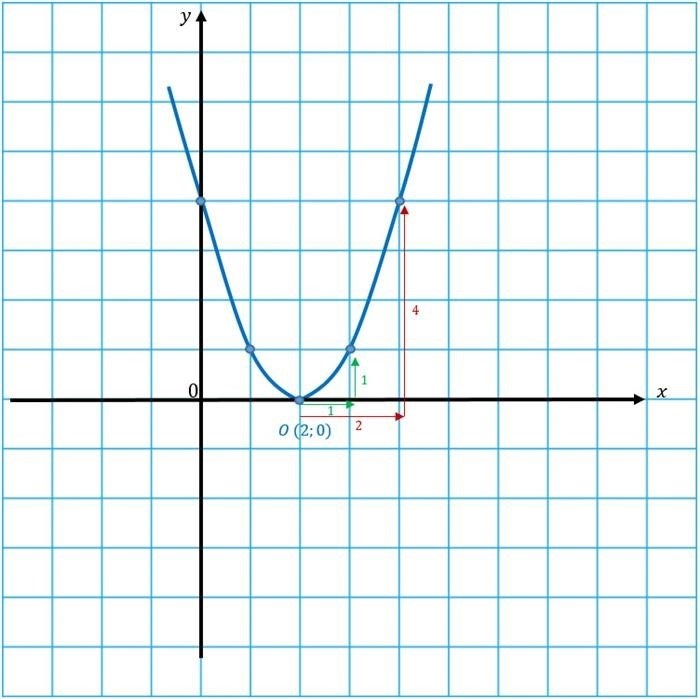
Квадратичная функция – это функция вида f(x) = ax 2 + bx + c, где a, b и c – коэффициенты, а x – переменная. График этой функции представляет собой параболу, которая может быть направленной вверх или вниз, в зависимости от значения коэффициента a. Изучение квадратичных функций и их графиков является важным элементом алгебры и анализа функций.
Муниципальное образовательное учреждение «Средняя общеобразовательная школа №3 г.Ершова Саратовской области»
Наша миссия:
- Обеспечить рост и развитие каждого ученика, учитывая его индивидуальные способности и потребности.
- Подготовить учащихся к успешной сдаче государственной итоговой аттестации.
- Формировать у детей навыки самостоятельного мышления, творческого и проектного подхода.
- Создать условия для социализации, формирования патриотических ценностей и гражданской ответственности.
Наши преимущества:
| Компетентный педагогический коллектив | В школе работают высококвалифицированные педагоги, постоянно совершенствующие свои знания и методики обучения. |
| Современные учебные материалы и оборудование | Школа оснащена современным оборудованием и обучающими материалами, которые позволяют эффективно проводить занятия. |
| Разнообразие внеурочной деятельности | В школе предлагаются различные кружки и секции, которые позволяют ученикам развивать свои таланты и интересы. |
В программе обучения школы уделяется особое внимание развитию математических навыков учащихся. Одной из основных тем является изучение квадратичной функции и ее графика.
Изучение квадратичной функции и ее графика:
- Основные определения и свойства квадратичной функции.
- Анализ графика квадратичной функции.
- Решение квадратных уравнений графическим и аналитическим методами.
- Применение квадратичной функции в жизненных ситуациях.
Изучение данной темы позволяет учащимся развить логическое мышление, умение анализировать и решать задачи в реальных ситуациях.
Муниципальное образовательное учреждение «Средняя общеобразовательная школа №3 г.Ершова Саратовской области» гордится своими достижениями и готова предложить каждому ребенку качественное образование.
Что такое функция?
Основные характеристики функции:
- Область определения: это множество значений аргумента, для которых функция определена.
- Область значений: это множество значений функции, которые она может принимать.
- Промежутки возрастания и убывания: это интервалы на оси аргумента, внутри которых функция возрастает или убывает.
- Экстремумы: это точки, в которых функция достигает максимального (минимального) значения.
- Симметрия: функция может быть симметричной относительно оси аргумента или оси значений.
- Асимптоты: это прямые, к которым функция стремится в бесконечности.
Примеры функций:
- Линейная функция: F(x) = kx + b, где k и b – коэффициенты, определяющие наклон и сдвиг графика.
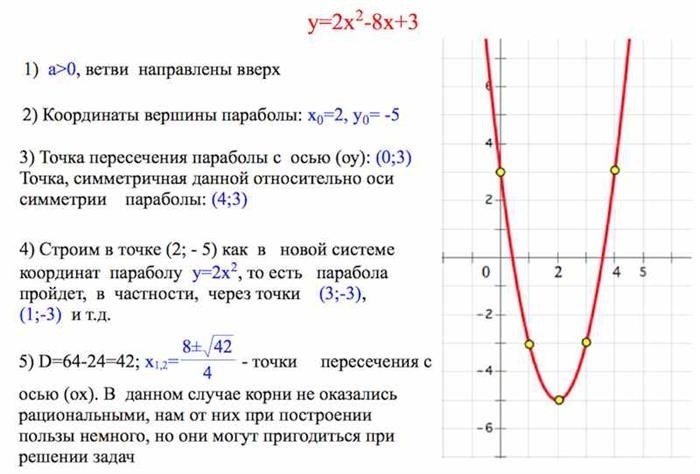
- Квадратичная функция: F(x) = ax 2 + bx + c, где a, b и c – коэффициенты, определяющие форму графика.
- Степенная функция: F(x) = x n, где n – степень, определяющая форму графика.
- Тригонометрическая функция: F(x) = sin(x), F(x) = cos(x), F(x) = tan(x) и другие, где sin, cos и tan – тригонометрические функции.
Функции играют важную роль в математике и других науках, так как позволяют описывать и анализировать различные явления и процессы. Знание функций позволяет решать уравнения, находить экстремумы, определять траектории движения и многое другое. Они также широко применяются в различных отраслях промышленности, информационных технологиях и финансовой сфере для моделирования и прогнозирования различных процессов и явлений.
| Тип преобразования | Формула | Описание |
|---|---|---|
| Горизонтальный сдвиг | F(x – a) | Сдвиг графика функции вправо на a единиц |
| Вертикальный сдвиг | F(x) + a | Сдвиг графика функции вверх на a единиц |
| Изменение масштаба по аргументу | F(kx) | Растяжение или сжатие графика функции вдоль оси аргумента |
| Изменение масштаба по значению | a * F(x) | Растяжение или сжатие графика функции вдоль оси значений |
| Отражение | -F(x) | Отражение графика функции относительно оси аргумента |
Понимание функций и их свойств позволяет анализировать и решать различные задачи, связанные с зависимостью величин друг от друга. Знание математических функций является важным компонентом образования и навыком, необходимым во многих областях деятельности.
Что называют квадратичной функцией
Квадратичная функция характеризуется несколькими важными свойствами:
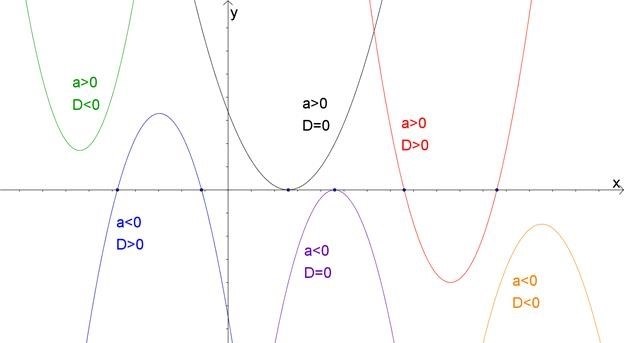
- Парабола, заданная квадратичной функцией, всегда открывается вверх или вниз, в зависимости от знака коэффициента a.
- Вершина параболы является экстремумом функции и является точкой минимума или максимума в зависимости от знака коэффициента a.
- Ось симметрии параболы проходит через вершину и параллельна оси ординат.
- График параболы симметричен относительно оси симметрии.
Квадратичные функции широко используются в математике и физике для моделирования различных явлений, включая движение тел, оптимизацию задач и прогнозирование данных. Изучение квадратичных функций позволяет понять и анализировать форму и поведение параболических кривых.