Вычитание в двоичной системе счисления является основным математическим действием, которое используется для обработки и анализа двоичных чисел. Правильное понимание процесса вычитания в двоичной системе позволяет легко выполнять сложные вычисления и решать задачи, связанные с бинарными числами.
Перевод десятичного числа в двоичное
Для перевода десятичного числа в двоичное необходимо следовать определенным шагам:
Шаг 1: Группировка разрядов
Десятичное число разбивается на разряды, начиная с самого правого разряда и двигаясь влево. Каждый разряд имеет свою степень значимости в десятичной системе счисления. Например, для числа 345, самый правый разряд будет единицей, следующий – десятком, а самый левый – сотнями.
Шаг 2: Деление числа на 2
Каждый разряд десятичного числа делится на 2. Результат деления записывается в двоичной системе счисления.

Шаг 3: Определение остатка
Остаток от деления каждого разряда записывается, начиная с самого правого. Если остаток равен 1, то этот разряд является значимым, если остаток равен 0, то разряд не значим.
Шаг 4: Повторение шагов 2-3
Процесс деления и определения остатка повторяется для каждого следующего разряда, начиная с правого и двигаясь влево.
Шаг 5: Запись двоичного числа
Результаты остатков записываются от самого левого значимого разряда до самого правого. Полученное число будет представлять десятичное число в двоичной системе счисления.
Например, для числа 345, процесс перевода выглядит следующим образом:
| Десятичное число | Двоичное число |
|---|---|
| 345 | 101011001 |
Таким образом, десятичное число 345 будет представлено в двоичной системе счисления как 101011001.
Сложение, вычитание и умножение двоичных чисел
Сложение двоичных чисел
Сложение двоичных чисел происходит по тому же принципу, что и сложение десятичных чисел. Нужно сложить каждую пару соответствующих битов и учесть возможное переносимое значение (единицу).
Рассмотрим пример сложения двоичных чисел:
| Число A | 1 | 0 | 1 | |
| Число B | 1 | 1 | 0 | |
| Сумма | 1 | 0 | 1 | (1) |
В результате сложения получаем число 1011, где (1) – переносимое значение.
Вычитание двоичных чисел
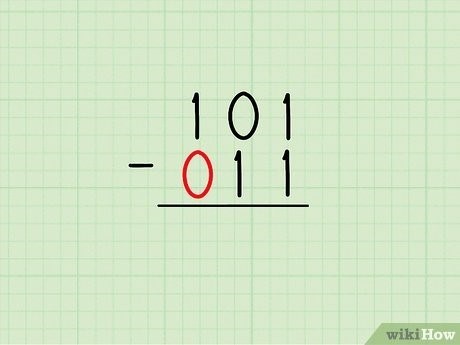
Вычитание двоичных чисел осуществляется аналогично вычитанию десятичных чисел. Необходимо вычитать каждый бит числа B из соответствующего бита числа A и учесть возможное заемное значение (единицу).
Рассмотрим пример вычитания двоичных чисел:
| Число A | 1 | 0 | 1 | |
| Число B | 1 | 1 | 0 | |
| Разность | 0 | 1 | 1 | (-1) |
В результате вычитания получаем число 011, где (-1) – заемное значение.
Умножение двоичных чисел
Умножение двоичных чисел выполняется по простым правилам умножения. Необходимо умножать каждый бит числа A на каждый бит числа B и складывать полученные произведения.
Рассмотрим пример умножения двоичных чисел:
| Число A | 1 | 0 | |
| Число B | 1 | 1 | |
| Произведение | 1 | 0 | |
| Произведение (ещё разряд) | 1 | 0 | 0 |
В результате умножения получаем число 1100.
Теперь вы знаете, как выполнять операции сложения, вычитания и умножения двоичных чисел. Применяйте эти знания в практике и укрепляйте свои навыки в работе с двоичной системой счисления.
Операция сдвига по разрядной сетке
Сдвиг вправо
При сдвиге вправо, все биты числа сдвигаются на указанное количество разрядов вправо. Старший бит (самый левый) заменяется нулем, а младший бит (самый правый) исчезает. Это эквивалентно делению числа на два в степени, которая равна количеству сдвигов. Например, сдвиг числа 1101 на два разряда вправо даст число 0011.
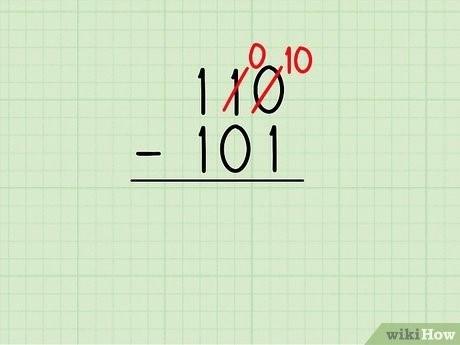
Сдвиг влево
При сдвиге влево, все биты числа сдвигаются на указанное количество разрядов влево. Младший бит (самый правый) заменяется нулем, а новый бит появляется в старшем разряде (самом левом). Это эквивалентно умножению числа на два в степени, которая равна количеству сдвигов. Например, сдвиг числа 0011 на два разряда влево даст число 1100.
Применение операции сдвига
Операция сдвига широко применяется в программировании и электронике. Вот несколько примеров:
- Умножение или деление чисел на степень двойки – сдвиг влево эквивалентен умножению на два, а сдвиг вправо эквивалентен делению на два.
- Обработка данных – сдвиг используется для сдвига или слияния битов, а также для манипулирования разрядами чисел.
- Управление данными – операция сдвига может быть использована для кодирования или декодирования информации, а также для передачи данных через различные интерфейсы.
Примеры операции сдвига
Вот несколько примеров операции сдвига:
| Число | Количество сдвигов | Сдвиг вправо | Сдвиг влево |
|---|---|---|---|
| 1010 | 2 | 0010 | 1000 |
| 0110 | 3 | 0000 | 0000 |
В первом примере число 1010 сдвигается на два разряда вправо, что приводит к получению числа 0010. Во втором примере число 0110 сдвигается на три разряда влево, что приводит к получению числа 0000.
Операция сдвига по разрядной сетке является важной и мощной операцией, которая используется во многих областях, связанных с двоичной системой счисления. Она позволяет эффективно управлять и обрабатывать данными, а также выполнять различные математические операции.
Примеры перевода чисел
Перевод чисел из одной системы счисления в другую имеет свои особенности и требует знания некоторых правил и алгоритмов. Рассмотрим несколько примеров перевода чисел из десятичной системы счисления в двоичную.
Пример 1
Переведем число 25 из десятичной системы счисления в двоичную. Для этого нужно разделить число нацело на 2 и записывать остатки от деления, начиная с последнего. Результатом будет являться число в обратном порядке. В итоге получаем:
- 25 / 2 = 12, остаток 1
- 12 / 2 = 6, остаток 0
- 6 / 2 = 3, остаток 0
- 3 / 2 = 1, остаток 1
- 1 / 2 = 0, остаток 1
Итак, число 25 в двоичной системе счисления будет равно 11001.

Пример 2
Возьмем число 67 и переведем его в двоичную систему счисления. Проведем аналогичные действия:
- 67 / 2 = 33, остаток 1
- 33 / 2 = 16, остаток 1
- 16 / 2 = 8, остаток 0
- 8 / 2 = 4, остаток 0
- 4 / 2 = 2, остаток 0
- 2 / 2 = 1, остаток 0
- 1 / 2 = 0, остаток 1
Таким образом, число 67 в двоичной системе счисления будет равно 1000011.
Пример 3
Рассмотрим число 173 и переведем его в двоичную систему счисления. Проводим аналогичные действия:
- 173 / 2 = 86, остаток 1
- 86 / 2 = 43, остаток 0
- 43 / 2 = 21, остаток 1
- 21 / 2 = 10, остаток 1
- 10 / 2 = 5, остаток 0
- 5 / 2 = 2, остаток 1
- 2 / 2 = 1, остаток 0
- 1 / 2 = 0, остаток 1
Таким образом, число 173 в двоичной системе счисления будет равно 10101101.
Об этой статье
В данной статье мы рассмотрели основные принципы вычитания в двоичной системе счисления. Мы изучили, что двоичные числа представляют собой комбинацию двух цифр 0 и 1, и как выполнять вычитание, используя правила вычитания из школьной математики. Также мы обсудили колоночный метод вычитания и его применение к двоичной системе.
Вычитание в двоичной системе счисления играет важную роль в компьютерных технологиях, так как позволяет выполнять операции вычитания с битами и байтами данных. Понимание этой темы необходимо для работы с битовыми операторами и выполнения алгоритмических задач, связанных с обработкой двоичных чисел.
В этой статье мы изучили основы вычитания в двоичной системе счисления и научились применять эти знания на практике. Мы рассмотрели различные методы вычитания в двоичной системе и их применение. Теперь вы можете применять эти знания для выполнения операций вычитания с двоичными числами и использовать их в своей работе с компьютером или программировании.