Расстояние между двумя точками на плоскости может быть подсчитано с использованием формулы расстояния в пространстве. Эта формула основана на теореме Пифагора и позволяет нам найти длину отрезка, соединяющего две точки, имеющих координаты (x1, y1) и (x2, y2). Использование этой формулы намного упрощает и ускоряет процесс определения расстояния на плоскости.
Формула расстояния между двумя точками на координатной плоскости
Общая формула
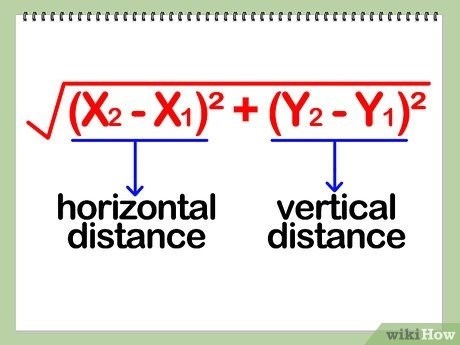
Формула расстояния между двумя точками на координатной плоскости:
d = √((x₂ – x₁)² + (y₂ – y₁)²)
где:
- d – расстояние между двумя точками;
- x₁, y₁ – координаты первой точки;
- x₂, y₂ – координаты второй точки.
Примеры использования
Давайте рассмотрим несколько примеров в качестве иллюстрации:
-
Если первая точка имеет координаты (1, 3), а вторая точка – (4, 6), то формула будет выглядеть следующим образом:
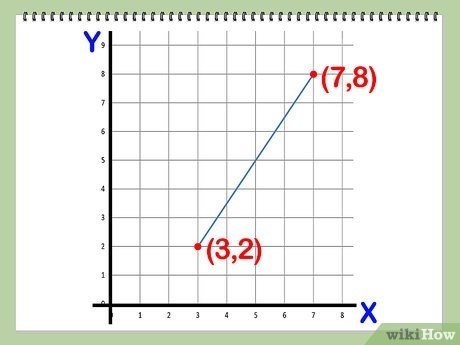
d = √((4 - 1)² + (6 - 3)²)
d = √(3² + 3²)
d = √(9 + 9)
d = √18
d ≈ 4.242
Таким образом, расстояние между этими двумя точками на координатной плоскости составляет примерно 4.242.
-
Если первая точка имеет координаты (-2, -5), а вторая точка – (-1, 3), то формула будет выглядеть следующим образом:
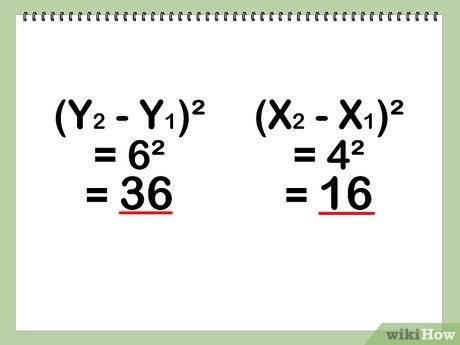
d = √((-1 - (-2))² + (3 - (-5))²)
d = √(1² + 8²)
d = √(1 + 64)
d = √65
d ≈ 8.062
Таким образом, расстояние между этими двумя точками на координатной плоскости составляет примерно 8.062.
Формула расстояния между двумя точками на координатной плоскости является полезным инструментом в различных областях, таких как геометрия, физика, прогнозирование движения объектов и других. Она помогает определить точное расстояние между объектами и может быть полезной для решения различных математических задач.

Расстояние между двумя точками прямой, плоскости и в пространстве
В данной статье мы рассмотрели различные способы вычисления расстояния между двумя точками на прямой, плоскости и в пространстве. Описали основные формулы и правила для каждого из случаев.
На прямой расстояние между двумя точками можно вычислить с помощью формулы модуля разности координат этих точек.

На плоскости используется формула расстояния между двумя точками, основанная на теореме Пифагора. Для этого необходимо найти разность координат по осям и применить формулу расстояния в декартовой системе координат.
В пространстве расстояние между двумя точками также вычисляется на основе формулы, основанной на теореме Пифагора. Для этого необходимо найти разность координат по осям и применить формулу расстояния в трехмерной системе координат.

Таким образом, расстояние между двумя точками на прямой, плоскости и в пространстве может быть вычислено с использованием различных формул, в зависимости от размерности системы координат. Эти формулы позволяют нам измерять расстояние и решать различные геометрические задачи.