Как решать дробно-рациональные уравнения

Дробно-рациональные уравнения являются одним из видов сложных уравнений, включающих в себя дробные выражения. Решение таких уравнений требует определенных навыков и методов. В данной статье вам будут представлены основные шаги и стратегии, которые помогут вам эффективно решать дробно-рациональные уравнения. Следуя этим рекомендациям, вы сможете легко и точно найти корни таких уравнений и получить полное решение. Ответы к задачам в данной статье представлены пошагово, что значительно облегчит вашу работу.

Рациональные уравнения – коротко о главном

1. Проверка на допустимость значений переменных

Перед решением рационального уравнения нужно проверить допустимость значений переменных. Если значения переменных приводят к знаменателю равному нулю, то решение уравнения не существует.

2. Приведение к общему знаменателю

Для удобства решения рационального уравнения, знаменатели дробей должны быть одинаковыми. Для этого необходимо привести уравнение к общему знаменателю. Если знаменатели уже одинаковые, можно перейти к следующему шагу.

3. Упрощение уравнения

При решении рационального уравнения необходимо упростить его до линейного или квадратного уравнения. Для этого можно сократить общие множители, использовать формулы приведения и другие алгебраические методы.

4. Решение упрощенного уравнения

После упрощения уравнения можно перейти к решению полученного уравнения. Если полученное уравнение линейное, решение можно найти с помощью метода подстановки или метода коэффициентов. Если уравнение квадратное, можно воспользоваться формулой дискриминанта или методом завершения квадрата.

5. Проверка полученного решения

После нахождения решения рационального уравнения, необходимо проверить его корректность, подставив найденное значение в исходное уравнение. Если значение подставленной переменной удовлетворяет уравнению, то решение верно.

Что такое рациональные уравнения?

P(x) / Q(x) = R(x) / S(x)

где P(x), Q(x), R(x) и S(x) – многочлены с переменной x.

• Многочлен: алгебраическое выражение, состоящее из произведения конечного числа переменных и констант, возведенных в неотрицательные целые степени, сложенных между собой.
• Уравнение: математическое выражение, описывающее равенство двух выражений.
• Рациональное: относящееся к отношению чисел, выраженному в виде дроби, где числитель и знаменатель являются многочленами.

Рациональные уравнения могут иметь одно или несколько решений, а также могут быть классифицированы как тождественно верные или неверные в зависимости от значения переменных в них.

Как решать рациональные уравнения?

Для решения рациональных уравнений необходимо провести следующие шаги:

1. Перенести все дроби на одну сторону уравнения, чтобы получить уравнение без дробей.
2. Домножить обе части полученного уравнения на общий знаменатель всех дробей, чтобы избавиться от знаменателей.
3. Раскрыть скобки и привести подобные члены в полученном уравнении.
4. Решить полученное уравнение для переменной.
5. Подставить найденные значения переменной обратно в исходные дроби, чтобы проверить правильность полученного решения.

Если переменная, для которой решается уравнение, находится в знаменателе дроби, необходимо проверить полученные значения на возможность обращения данной дроби в ноль. Если значение переменной делает знаменатель равным нулю, то такое значение нужно исключить из множества решений уравнения.

Решение рациональных уравнений может быть выражено в виде конечного множества значений переменной или в виде условия на переменную, при котором уравнение тождественно верно или неверно. Всегда стоит проверять решение на корректность и возможность его применения к заданным условиям.

Пример рационального уравнения:

Рассмотрим пример рационального уравнения:

(3x – 4) / (2x + 1) = 5 / (x – 2)

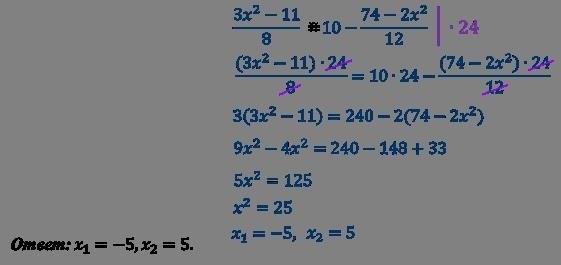
Для его решения выполним следующие шаги:

1. Перенесем дроби на одну сторону:

(3x – 4) / (2x + 1) – 5 / (x – 2) = 0

2. Домножим обе части уравнения на общий знаменатель (2x + 1)(x – 2):

(3x – 4)(x – 2) – 5(2x + 1) = 0

3. Раскроем скобки и приведем подобные члены:

3x 2 – 6x – 4x + 8 – 10x – 5 = 0

4. Решим полученное квадратное уравнение:

3x 2 – 20x + 3 = 0

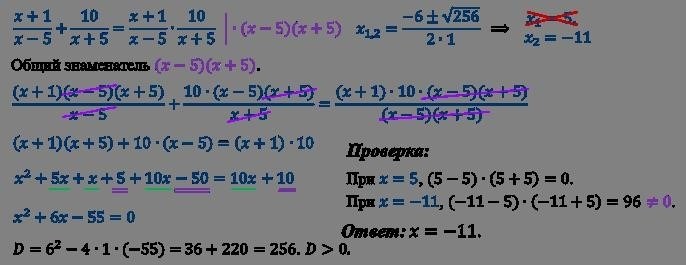
Используя формулу дискриминанта, найдем значения переменной x:

x = (-b ± √(b 2 – 4ac)) / (2a)

Подставив коэффициенты a, b и c из уравнения, мы найдем два возможных значения x:

x = (20 ± √(20 2 – 4 * 3 * 3)) / (2 * 3)

Решив это уравнение, мы получим два значения переменной x:

x1 ≈ 0.372

x2 ≈ 6.96

5. Проверим полученное решение, подставив значения переменной в исходное уравнение:

(3 * 0.372 – 4) / (2 * 0.372 + 1) = 5 / (0.372 – 2)

(3 * 6.96 – 4) / (2 * 6.96 + 1) = 5 / (6.96 – 2)

Если полученные значения равны друг другу, то решение верно.

Рациональные уравнения – это уравнения с дробными выражениями, содержащими переменные в числителе и знаменателе. Их решение требует переноса дробей на одну сторону уравнения, домножения обеих частей на общий знаменатель, раскрытия скобок и приведения подобных членов, а затем решения полученного алгебраического уравнения. При решении необходимо учитывать условия, чтобы исключить некорректные значения переменной, а также проверить полученное решение, чтобы убедиться в его правильности.

Алгоритм решения рационального уравнения

Алгоритм решения рационального уравнения состоит из следующих шагов:

1. Перенесите все слагаемые на одну сторону уравнения так, чтобы уравнение стало равным нулю.
2. Упростите полученное уравнение, приведя подобные слагаемые и сокращая дроби.
3. Приведите уравнение к общему знаменателю, если в уравнении присутствуют дроби с разными знаменателями.
4. Разложите полученное уравнение на множители и установите значения переменных, при которых каждый из множителей равен нулю.
5. Для каждого полученного значения переменной проверьте, является ли оно корнем уравнения.

После применения указанных шагов вы получите корни рационального уравнения. Чтобы проверить правильность полученных корней, подставьте их в исходное уравнение и убедитесь, что обе его части совпадают.