Разделение натурального числа на десятичную дробь может быть выполнено путем последовательного перемещения запятой влево на столько разрядов, сколько требуется поделить число.
Перенос запятой при делении на десятичную дробь
При делении натурального числа на десятичную дробь необходимо правильно разместить запятую, чтобы получить точный результат. В этом случае необходимо учитывать различные правила и особенности. Рассмотрим подробнее, как это сделать.
1. Разделение на целую и десятичную части
Перед тем, как начать деление, нужно определить, какая часть числа будет являться целой, а какая – десятичной. Это зависит от того, сколько знаков после запятой в ответе вы хотите получить. Если вы хотите получить ответ с определенным количеством знаков после запятой, рассмотрим следующие правила.
2. Деление с заданным количеством знаков после запятой
Если вы хотите получить ответ с определенным количеством знаков после запятой, то нужно следующее:
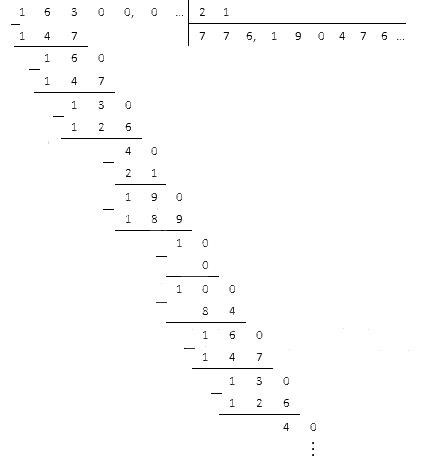
- В основном делении числа, перед делением, добавлять ноль, чтобы обозначить, что десятичная часть отсутствует. Например, если число 35, то перед делением будет 35,0.
- Провести деление, как обычно. Запятая в ответе будет находиться в том же месте, что и в делителе. Если в делителе запятая находится на 1-м знаке справа от начала числа, то и в ответе запятая будет находиться на 1-м знаке слева от начала числа.
- Полученный ответ дополнить нулями справа до нужного количества знаков после запятой.
3. Примеры
| Число | Делитель | Ответ |
|---|---|---|
| 35,0 | 5 | 7,00 |
| 50,0 | 4 | 12,50 |
| 100,0 | 10 | 10,00 |
Перенос запятой при делении на десятичную дробь требует внимания к деталям. Следуя правилам, вы сможете получить точный результат с нужным количеством знаков после запятой. Не забывайте дополнять ответы нулями справа до нужного количества знаков после запятой, чтобы быть уверенным в точности результата. Используйте приведенные примеры для лучшего понимания. Удачи в расчетах!
Деление десятичной дроби на другую десятичную дробь
Деление одной десятичной дроби на другую десятичную дробь можно выполнить с помощью простого алгоритма, следуя определенной последовательности действий. В этом процессе важно осознавать правила и свойства десятичных дробей, чтобы получить точный результат.
Шаги деления десятичной дроби на другую десятичную дробь:
- Упростите дроби, если это возможно. Сократите общие делители числителя и знаменателя дробей до простейших дробей.
- Умножьте числитель первой дроби на знаменатель второй дроби и числитель второй дроби на знаменатель первой дроби. Получите две новые дроби.
- Сравните полученные новые дроби и определите, какая из них больше. Это позволит определить результат деления.
Пример:
- Рассмотрим деление десятичной дроби 0,36 на десятичную дробь 0,12.
- Упростим дроби: 0,36 = 36/100 и 0,12 = 12/100.
- Произведем умножение: (36/100) * (100/12) = 36/12 = 3.
- Таким образом, результатом деления 0,36 на 0,12 равен 3.
Деление десятичной дроби на другую десятичную дробь требует умножения числителей и знаменателей дробей и сравнения полученных значений. Соблюдение правил и свойств десятичных дробей поможет получить точный результат. Важно помнить о простоте и удобстве выбранного алгоритма, который позволяет выполнить деление максимально эффективно.
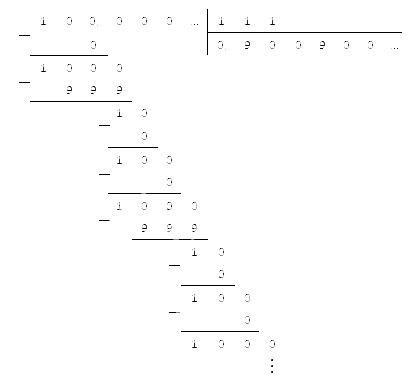
Правило деления числа на десятичную дробь
Правило деления числа на десятичную дробь:
- Переписываем делитель (десятичную дробь) так, чтобы у нее было столько же разрядов после запятой, сколько и у делимого числа.
- Подводим делитель к делимому, ставим их в столбик и проводим штриховку.
- Начиная с самого левого разряда делимого числа, делим его на первую цифру делителя.
- Полученное частное записываем над делителем и умножаем его на делитель.
- Вычитаем полученное произведение из делимого и переносим остаток в следующий разряд.
- Повторяем шаги 3-5 для всех разрядов делимого числа.
- Если у делимого числа больше нет следующего разряда, и остаток равен нулю, то деление завершается.
- Если остаток не равен нулю, то добавляем ноль после запятой и переходим к следующему разряду.
В результате правильного применения правила деления числа на десятичную дробь, мы получим точное значение частного и остатка. Это позволяет нам проводить дальнейшие математические операции или использовать полученные результаты для решения конкретных задач.
Основы деления десятичных дробей
Правила деления десятичных дробей:
- Первым делом, необходимо записать делимое и делитель в виде десятичных дробей.
- Затем нужно придать делителю вид целого числа, переместив запятую вправо такое количество раз, чтобы получилось натуральное число.
- После этого, необходимо переместить запятую в делимом такое же количество раз в том же направлении.
- Затем выполнить деление натурального числа без остатка и записать результат.
- Если после деления остается остаток, то запятую нужно поставить в частном после стольких разрядов, сколько заняло операций деления.
- Разделить остаток на делитель, придав ему вид натурального числа с запятой, и продолжить деление, пока остаток не станет равным нулю или не будет повторяться.
- Итоговый результат деления будет представлять собой частное и десятичную дробь.
Пример деления десятичных дробей:
Допустим, мы хотим разделить число 5 на десятичную дробь 0.2. Следуя правилам, мы получаем следующие шаги:
- Записываем делимое (5) и делитель (0.2) в виде десятичных дробей: 5 / 0.2
- Перемещаем запятую в делителе, чтобы получить натуральное число: 5 / 0.2 = 5 / 2
- Перемещаем запятую в делимом: 5 / 2 = 50 / 2
- Выполняем деление: 50 / 2 = 25
- Результат деления без остатка: 25
В данном примере, результатом деления является число 25 без десятичных знаков. Это означает, что итоговый результат деления будет представлять собой частное, равное 25, и десятичную дробь, которая равна нулю.
Деление натурального числа на десятичную дробь: итог
В данной статье мы рассмотрели способы деления натурального числа на десятичную дробь.
Вначале мы ознакомились с понятием десятичной дроби и ее записью, а также разобрали метод деления столбиком. Затем мы изучили алгоритм десятичного деления, который включает в себя поэтапное вычитание десятичной дроби из натурального числа.
- Шаг 1: Расставляем нули после запятой в натуральном числе, чтобы оно имело столько же разрядов после запятой, сколько и десятичная дробь.
- Шаг 2: Вычитаем десятичную дробь из полученного числа, начиная с самого левого разряда.
- Шаг 3: Если в результате вычитания получается отрицательное число, занимаем единицу из предыдущего разряда натурального числа.
- Шаг 4: Продолжаем вычитать десятичную дробь из полученного числа, выполняя шаги 2-3 до тех пор, пока не получим ответ с требуемой точностью.
Используя данный алгоритм, мы можем делить натуральное число на десятичную дробь с любой заданной точностью. Такой подход особенно полезен при решении задач, связанных с финансами, процентными ставками и другими ситуациями, требующими точного деления на десятичные дроби.
Следует отметить, что этот метод деления требует определенной точности и аккуратности в вычислениях, поэтому при использовании его в реальных ситуациях необходимо быть внимательным и проверять полученные результаты.