Угол между прямой и плоскостью можно рассчитать при помощи векторных операций. Сначала необходимо определить векторы, соответствующие прямой и плоскости, а затем использовать формулу для вычисления угла между векторами. Этот метод позволяет точно определить угол и использовать его в дальнейших вычислениях или задачах на геометрию.
Свойства и теоремы
1. Угол между прямой и плоскостью
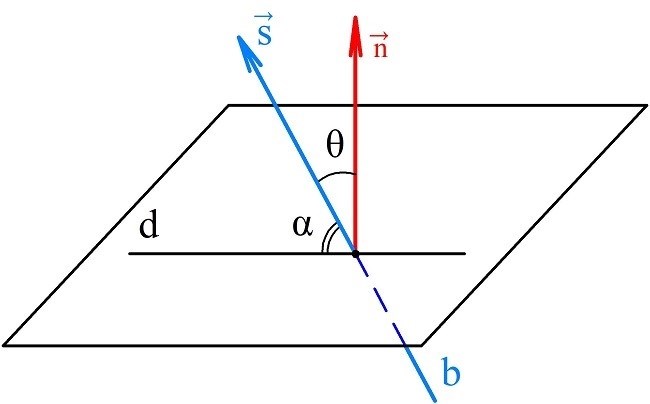
Угол между прямой и плоскостью определяется как угол между прямой, проходящей через заданную точку на плоскости, и нормалью к этой плоскости.
2. Нормаль и направляющий вектор
Нормаль к плоскости – это вектор, перпендикулярный плоскости. Направляющий вектор прямой – это вектор, указывающий вдоль прямой.
3. Угол между векторами
Угол между векторами определяется как угол между направляющими векторами прямой и нормалью к плоскости.
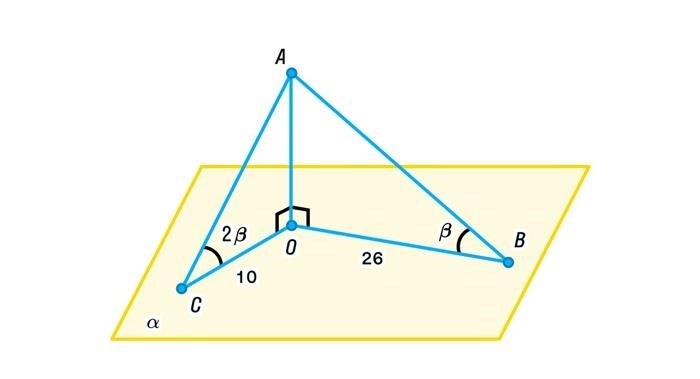
4. Формула для вычисления угла
Угол между прямой и плоскостью можно вычислить с использованием следующей формулы:
cos(угол) = |ск(вектор_нормали, вектор_прямой)| / (|вектор_нормали| * |вектор_прямой|)
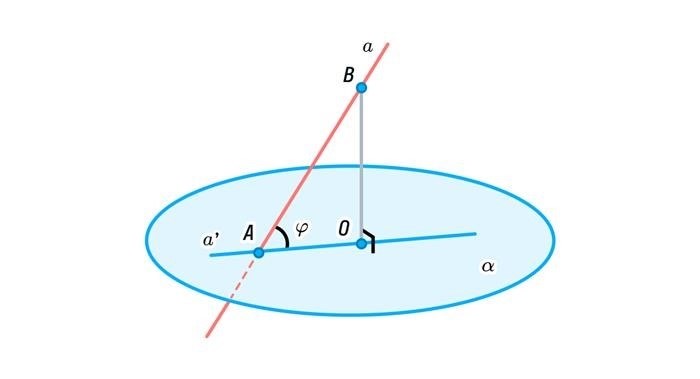
5. Угол между пересекающимися прямой и плоскостью
Если прямая пересекает плоскость, то угол между ними равен нулю, так как вектор прямой лежит в плоскости.
6. Угол между параллельными прямой и плоскостью
Если прямая параллельна плоскости, то угол между ними равен 90 градусов, так как направляющий вектор прямой перпендикулярен вектору нормали плоскости.
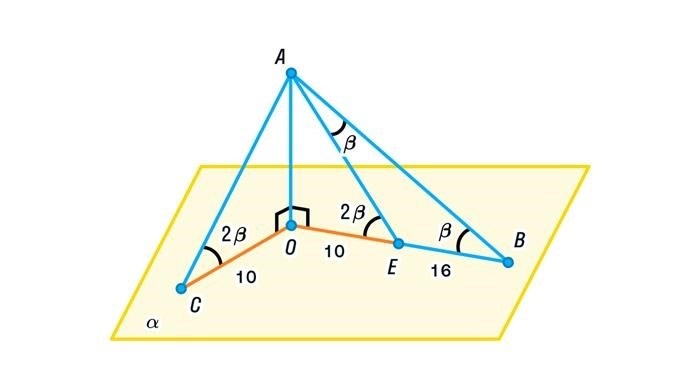
7. Теорема о перпендикулярности прямой и плоскости
Прямая перпендикулярна плоскости, если и только если ее направляющий вектор перпендикулярен вектору нормали плоскости.
8. Задание прямой в пространстве
Прямая в пространстве может быть задана двумя способами: либо через координаты двух точек на ней, либо через направляющий вектор и точку на прямой.
9. Задание плоскости
Плоскость может быть задана через ее нормаль и точку на плоскости или через три точки, не лежащие на одной прямой.
Изучение свойств и теорем, связанных с углом между прямой и плоскостью, поможет решить задачи, связанные с этой темой в геометрии.
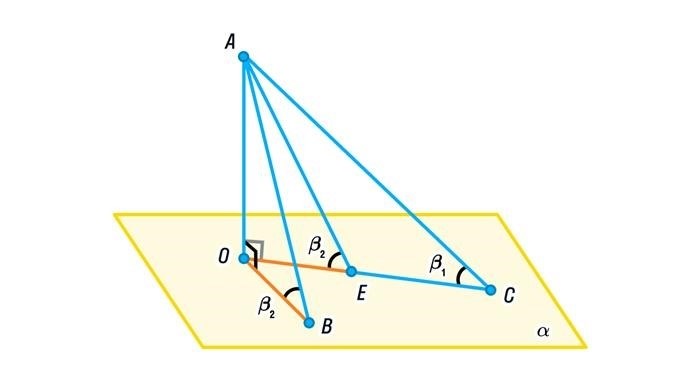
Теорема о трех перпендикулярах
Теорема о трех перпендикулярах является одним из основных результатов в трехмерной геометрии. Она позволяет рассматривать взаимосвязь между прямыми и плоскостями и использовать их в решении различных геометрических задач.
Выведение данной теоремы основано на свойствах перпендикуляров и плоскостей, и может быть доказано с использованием геометрической арифметики. Теорема о трех перпендикулярах имеет множество приложений в различных областях математики и физики, включая аналитическую геометрию, механику и строительство.
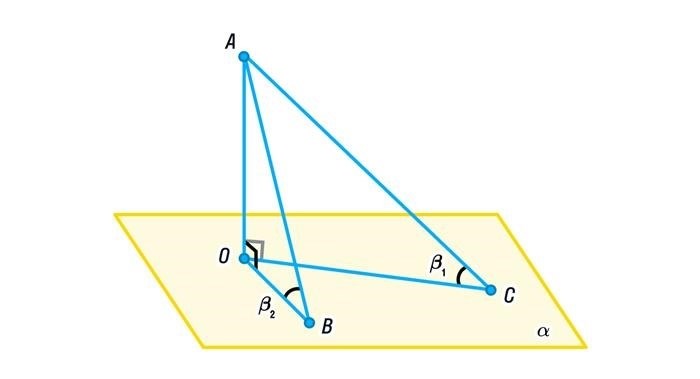
Таким образом, теорема о трех перпендикулярах является важным утверждением в геометрии, которое позволяет рассматривать взаимосвязь между прямыми и плоскостями и использовать ее в решении различных задач. Она открывает новые возможности для изучения трехмерной геометрии и применения ее в практических ситуациях.