Расстояние от точки до плоскости – это величина, которая позволяет определить, насколько далеко находится заданная точка от данной плоскости. Зная координаты точки и уравнение плоскости, мы можем вычислить это расстояние.
Существует несколько способов нахождения расстояния между точкой и плоскостью:
1. Геометрический подход
Для начала, мы можем применить геометрический подход, используя формулу:
d = |Ax + By + Cz + D| / sqrt(A 2 + B 2 + C 2),
где (x, y, z) – координаты точки, A, B, C – коэффициенты уравнения плоскости и D – свободный член.
2. Векторный подход
Векторный подход более эффективен при работе с векторами. Мы можем использовать следующую формулу:
d = |(P – P0) * n| / |n|,
где P – координаты точки, P0 – точка на плоскости, n – нормальный вектор плоскости.
Векторный подход позволяет найти расстояние между точкой и плоскостью с использованием векторных операций.
Важно помнить, что для правильного вычисления расстояния от точки до плоскости необходимо знать координаты точки и уравнение плоскости. При неправильных данных результат может быть некорректным.
Итак, мы рассмотрели два основных подхода к нахождению расстояния от точки до плоскости – геометрический и векторный. Выбор подхода зависит от постановки задачи и предпочтений программиста или математика.
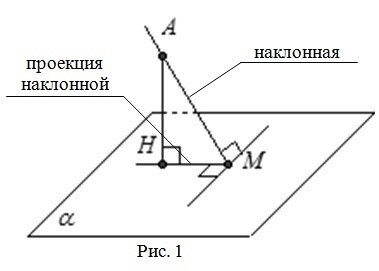
Теорема о трех перпендикулярах
Суть теоремы заключается в следующем:
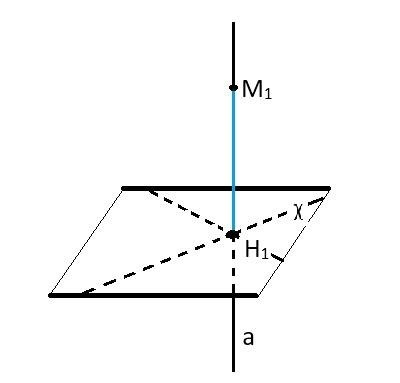
- Если прямая AB перпендикулярна к плоскости P, и прямая AB пересекает эту плоскость в точке O, то любая прямая, проходящая через точку O и перпендикулярная к плоскости P, будет перпендикулярна ко всем прямым, лежащим в плоскости P, и проходящим через точку O.
- Если прямая AB перпендикулярна к отрезку CD, и точка C лежит на этой прямой, то любая прямая, проходящая через точку C и перпендикулярная к отрезку CD, будет перпендикулярна ко всем отрезкам, имеющим общий конец в точке C.
- Если плоскость P1 перпендикулярна к плоскости P2 в точке O, и плоскость P1 пересекает плоскость P2 по прямой AB, то любая прямая, лежащая в плоскости P1 и проходящая через точку O, будет перпендикулярна ко всем прямым, лежащим в плоскости P2 и проходящим через точку O.
Теорема о трех перпендикулярах имеет множество практических применений в геометрии и технике. Она используется для решения задач по построению перпендикуляров, определению расстояний и углов, а также при проектировании и изготовлении различных конструкций.