Как найти расстояние между прямыми

Расстояние между двумя параллельными прямыми или пересекающимися прямыми можно вычислить с помощью геометрии и алгебры. Для параллельных прямых достаточно найти расстояние между ними, используя уравнения прямых. Если прямые пересекаются, то для вычисления расстояния необходимо найти координаты пересечения и применить формулу расстояния между двумя точками.

Методика вычисления расстояния между прямыми

Метод 1: Формула расстояния от точки до прямой

Для начала необходимо выбрать точку на первой прямой, например A, и провести от нее перпендикуляр к второй прямой. Затем находим точку пересечения перпендикуляра с второй прямой, которую обозначим B. Расстояние между прямыми будет равно расстоянию от точки A до точки B.

Формула: d = |(Ax – Bx) * n1 + (Ay – By) * n2| / sqrt(n1 2 + n2 2), где (Ax, Ay) и (Bx, By) – координаты точек A и B, а n1 и n2 – коэффициенты уравнения прямой.

Метод 2: Формула расстояния между параллельными прямыми

Если прямые параллельны, то расстояние между ними можно найти по формуле:

Формула: d = |c1 – c2| / sqrt(a 2 + b 2), где a, b и c1, c2 – коэффициенты уравнений для первой и второй прямых соответственно.

Метод 3: Формула расстояния между скрещивающимися прямыми

Если прямые пересекаются, то для вычисления расстояния нужно применить другую формулу:

Формула: d = 0, если прямые пересекаются

Важно отметить, что вычисление расстояния между прямыми может быть сложным в некоторых случаях, особенно при непрямых уравнениях или наличии дополнительных условий. Для точного определения расстояния рекомендуется использовать необходимые формулы и методы, а также проводить проверку результатов на соответствие задаче.

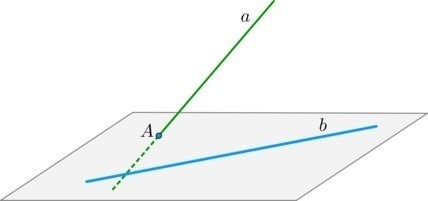
Взаимное расположение прямой и плоскости

Взаимное расположение прямой и плоскости может быть разным в зависимости от их геометрических характеристик и взаимного расположения в пространстве. Рассмотрим основные случаи взаимного расположения этих геометрических фигур.

1. Прямая пересекает плоскость

Если прямая пересекает плоскость, то они имеют общую точку. В этом случае, расстояние между прямой и плоскостью равно нулю.

2. Прямая параллельна плоскости

Если прямая не пересекает плоскость, но лежит в параллельном ей направлении, то расстояние между прямой и плоскостью можно найти с помощью следующей формулы:

Расстояние = |D – D0| / √(A 2 + B 2 + C 2)

где A, B, C – коэффициенты плоскости, D – расстояние от начала координат до плоскости, D0 – смещение плоскости от начала координат.

3. Прямая скользит вдоль плоскости

Если прямая лежит в плоскости, то расстояние между ними будет равно нулю. В этом случае, прямая “скользит” вдоль плоскости.

Пример взаимного расположения прямой и плоскости:

Прямая	Плоскость	Взаимное расположение
Пересекает плоскость	Пересекает прямую	Общая точка пересечения
Пересекает плоскость	Не пересекает прямую	Расстояние между прямой и плоскостью равно нулю
Параллельна плоскости	Не пересекает прямую	Расстояние между прямой и плоскостью может быть найдено с помощью формулы
Скользит вдоль плоскости	Не пересекает прямую	Расстояние между прямой и плоскостью равно нулю

Взаимное расположение прямой и плоскости в пространстве может быть важным фактором при решении геометрических задач и нахождении расстояний между ними. Учитывая их взаимное положение, можно более точно определить геометрические характеристики объектов и поверхностей.

Угол между прямой и плоскостью

Способы нахождения угла между прямой и плоскостью:

• Использование векторов: угол между прямой и плоскостью можно выразить с помощью скалярного произведения векторов, которые задают прямую и нормаль плоскости;
• Применение уравнений прямой и плоскости: угол между прямой и плоскостью можно найти, используя уравнения прямой и плоскости. Для этого необходимо свести задачу к нахождению угла между вектором, перпендикулярным плоскости, и вектором, параллельным прямой;
• Геометрический метод: угол между прямой и плоскостью можно визуализировать на чертеже. Для этого необходимо построить перпендикуляр к плоскости из точки прямой, а затем провести линию, соединяющую эту точку с точкой пересечения перпендикуляра с плоскостью;

Пример нахождения угла между прямой и плоскостью:

Допустим, дана прямая, заданная уравнением l: (x – 1)/2 = (y + 2)/3 = (z – 3)/4, и плоскость, заданная уравнением П: 2x – y + z – 5 = 0. Необходимо найти угол между этой прямой и плоскостью.

Способ решения:

1. Найдем вектор направления прямой. Для этого возьмем коэффициенты при x, y и z в уравнении прямой и составим вектор AB: AB: (1, 2, 3);
2. Найдем нормаль к плоскости. Для этого возьмем коэффициенты при x, y и z в уравнении плоскости и составим вектор b: b: (2, -1, 1);
3. Найдем скалярное произведение векторов AB и b. Для этого воспользуемся формулой: cos(угол) = (AB · b) / (|AB| * |b|);
4. Подставим значения в формулу и рассчитаем угол между прямой и плоскостью.

С помощью вышеуказанных методов можно находить угол между прямой и плоскостью в различных задачах, что позволяет углубить понимание их взаимоотношений и использовать в дальнейших вычислениях.

Курсовые работы, написанные преподавателями ВУЗов: качество и преимущества

Профессиональный подход специалистов

Курсовые работы, написанные действующими преподавателями ВУЗов, отличаются высоким качеством и профессиональным подходом к их выполнению. Эти специалисты обладают глубокими знаниями в своих областях и имеют опыт преподавания, что позволяет им предложить студентам актуальные и содержательные темы для исследования.

Преимущества курсовых работ, написанных преподавателями

Какие преимущества имеют курсовые работы, написанные действующими преподавателями ВУЗов?

• Глубокие знания и экспертиза: Преподаватели, работающие в ВУЗах, обладают актуальными знаниями в своей предметной области и следят за последними тенденциями. Используя свою экспертизу, они помогают студентам создавать качественные работы с актуальным материалом.
• Индивидуальный подход: Преподаватели знают особенности своих студентов и могут предложить индивидуальные темы для исследования, учитывая их интересы и потребности.
• Оценка согласно требованиям ВУЗа: Такие курсовые работы отвечают требованиям и стандартам, установленным ВУЗом. Преподаватели знают ожидания и требования своего учебного заведения, поэтому работы, написанные ими, соответствуют этим критериям.

Курсовые работы, написанные действующими преподавателями ВУЗов, представляют особую ценность для студентов. Эти работы отличаются высоким качеством, профессиональным подходом и соответствием требованиям учебных заведений. Студенты, обращаясь к таким специалистам за помощью, могут быть уверены в получении актуальной и качественной работы, которая будет соответствовать ожиданиям преподавателей. Это поможет им успешно завершить свои учебные программы и достичь своих учебных целей.

Угол между прямыми

Существует несколько способов вычисления угла между прямыми. Рассмотрим наиболее распространенные методы:

Метод использования угловых коэффициентов

Угловой коэффициент прямой определяется как отношение изменения координат по оси y к изменению координат по оси x.

Для двух прямых, угол между которыми нужно вычислить, можно вычислить угловые коэффициенты каждой из них и затем использовать формулу tan(α) = |(m₂ – m₁) / (1 + m₁m₂)|, где m₁ и m₂ – угловые коэффициенты прямых.

Метод использования векторного произведения

Другой способ вычисления угла между прямыми основан на использовании векторного произведения.

Пусть прямые заданы в параметрической форме: l₁: P₁ + t₁ v₁ и l₂: P₂ + t₂ v₂, где P₁ и P₂ – точки, лежащие на соответствующих прямых, v₁ и v₂ – направляющие векторы прямых, t₁ и t₂ – параметры.

Угол между прямыми может быть найден с использованием формулы cos(α) = |v₁ × v₂| / (|v₁| × |v₂|), где |v₁| и |v₂| – длины векторов v₁ и v₂.

Пример вычисления угла между прямыми

Для наглядности рассмотрим пример. Пусть даны две прямые:

• Прямая l₁: y = 2x + 1
• Прямая l₂: y = -0.5x + 3

Вычислим угол между этими прямыми используя формулу с угловыми коэффициентами:

Угловые коэффициенты прямых:

• m₁ = 2
• m₂ = -0.5

Подставим значения в формулу tan(α) = |(m₂ – m₁) / (1 + m₁m₂)|:

tan(α) = |(-0.5 – 2) / (1 + 2 * -0.5)| = |-2.5 / (1 – 1)| = 2.5

Далее, найдем значение угла α в градусах, используя тригонометрическую функцию обратного тангенса.

α = arctan(2.5) ≈ 67.38°

Таким образом, угол между прямыми l₁ и l₂ составляет примерно 67.38°.

Метод координат для определения расстояния

Шаг 1: Находим уравнение прямых

Сначала необходимо найти уравнения двух прямых, расстояние между которыми хотим определить. Уравнение прямой можно записать в виде y = mx + b, где m – угловой коэффициент прямой, а b – свободный член. Для этого нужно знать координаты двух точек на прямой или хотя бы одну точку и угловой коэффициент.

Шаг 2: Находим перпендикулярные прямые

Далее необходимо найти две перпендикулярные прямые, которые проходят через каждую из исходных прямых. Для этого можно использовать условие равенства произведений угловых коэффициентов двух прямых, проходящих через одну точку.

Шаг 3: Находим точку пересечения перпендикулярных прямых

Затем нужно найти точку пересечения перпендикулярных прямых. Для этого решаем систему уравнений, составленную из уравнений перпендикулярных прямых. Полученные координаты точки пересечения будут являться точкой на исходных прямых, через которую проходит перпендикуляр.

Шаг 4: Рассчитываем расстояние между пересечениями

Наконец, рассчитываем расстояние между точками пересечения и точками, через которые проходят исходные прямые. Для этого используем формулу расстояния между двумя точками в декартовой системе координат.

Пример

Рассмотрим пример для наглядности. Пусть у нас есть две прямые с уравнениями: y = 2x + 1 и y = -3x + 4. Находим перпендикулярные прямые, которые проходят через каждую из исходных прямых: y = -0.5x + 2.5 и y = 0.5x – 0.5. Находим точку пересечения этих двух перпендикулярных прямых: (1, 2). Теперь можем рассчитать расстояние между точками пересечения и точками (1, 3) и (2, 5) на исходных прямых.

Полученный результат

Расстояние между прямыми y = 2x + 1 и y = -3x + 4 составляет 1.41 единицы.

Определение прямых для нахождения расстояния

Для нахождения расстояния между двумя прямыми необходимо определить их уравнения и используя определенные формулы вычислить данную величину.

Определение уравнений прямых

Прямые обычно задаются уравнениями вида y = kx + b, где k – коэффициент наклона прямой, а b – свободный член.

Существуют несколько способов определения уравнений прямых:

• По двум точкам, через которые проходит прямая;
• По одной точке и направляющему вектору;
• Из уравнения прямой, заданного в параметрической форме.

Нахождение расстояния между прямыми

Существует несколько формул для вычисления расстояния между прямыми:

• Формула, основанная на нахождении расстояния от одной точки одной прямой до другой прямой;
• Формула, основанная на вычислении модуля проекции вектора, перпендикулярного одной из прямых, на направляющий вектор другой прямой.

Для точных вычислений рекомендуется использовать формулу, основанную на вычислении модуля проекции вектора.

Формула	Описание
d = |(A2 – A1) × n| / |n|	Формула, где A1 и A2 – заданные точки на прямых, n – направляющий вектор одной из прямых.

Пример

Даны две прямые с уравнениями:

• Прямая 1: y = 2x + 1
• Прямая 2: y = -3x + 4

Необходимо найти расстояние между данными прямыми.

Для решения данной задачи воспользуемся формулой:

• d = |(A2 – A1) × n| / |n|

Выберем точку A1 = (0,1) на Прямой 1 и точку A2 = (0,4) на Прямой 2. Направляющий вектор прямой 1 равен n = (1,2).

Подставим значения в формулу и произведем вычисления:

• d = |(0,4 – 0,1) × (1,2)| / |(1,2)|
• d = |(0,3) × (1,2)| / |(1,2)|
• d = |0,36| / |(1,2)|
• d = 0,36 / 1,44
• d ≈ 0,25

Таким образом, расстояние между прямыми составляет приблизительно 0,25 единицы длины.

Метод координат для определения расстояния между скрещивающимися прямыми

Для начала, необходимо найти точку пересечения прямых, для чего решим систему уравнений, составленную из уравнений данных прямых. Получив координаты точки пересечения, можно применить формулу для нахождения расстояния между этой точкой и любой из заданных прямых.

Итоговый алгоритм для определения расстояния между скрещивающимися прямыми:

1. Записать уравнения прямых.
2. Решить систему уравнений, чтобы найти точку пересечения прямых.
3. Выбрать одну из заданных прямых и рассчитать расстояние от точки пересечения до нее, используя формулу для расстояния между двумя точками.

Таким образом, метод координат позволяет определить расстояние между скрещивающимися прямыми, используя их уравнения и нахождение точки пересечения. Этот метод является достаточно простым и понятным, позволяя решать такие задачи без необходимости использования сложных геометрических конструкций.