Общий делитель – это число, которое делит нацело два или более числа. Найти общий делитель двух чисел можно с помощью нескольких методов, включая проверку деления чисел на все их возможные делители, а также использование алгоритма Евклида. Зная общие делители двух чисел, можно решать различные задачи, такие как сокращение дробей или нахождение наименьшего общего кратного.
Что такое НОД?
Нахождение НОД является важной задачей в математике и прикладных науках. Он используется, например, в криптографии, алгоритмах сжатия данных, оптимизации и других областях.
Способы нахождения НОД
- Метод проверки делителями: данный метод основан на поочередной проверке всех возможных делителей чисел. НОД будет равен наибольшему числу, которое делит оба числа без остатка.
- Метод разложения на множители: данный метод основан на разложении чисел на простые множители и нахождении их общих простых множителей.
- Алгоритм Евклида: данный алгоритм основан на последовательных делениях двух чисел и нахождении НОД при помощи остатков от делений.
Пример нахождения НОД методом Евклида
Рассмотрим два числа 54 и 24:
| Шаг | Делимое | Делитель | Остаток от деления |
|---|---|---|---|
| 1 | 54 | 24 | 6 |
| 2 | 24 | 6 | 0 |
По алгоритму Евклида НОД будет равен последнему ненулевому остатку, который в данном случае равен 6. Таким образом, НОД чисел 54 и 24 равен 6.
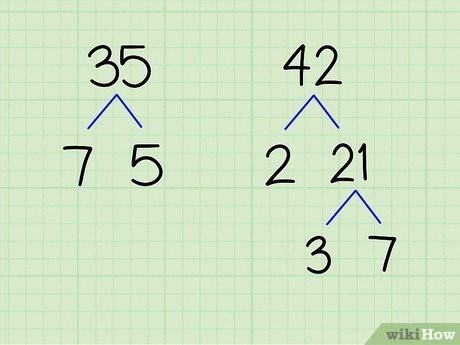
Нахождение путём разложения на множители
Шаги по нахождению общего делителя путём разложения на множители:
- Разложите каждое число на простые множители.
- Определите общие простые множители двух чисел.
- Умножьте общие простые множители друг на друга.
- Полученное произведение будет являться общим делителем двух чисел.
Рассмотрим пример нахождения общего делителя двух чисел 24 и 36:
| Число | Разложение на множители |
|---|---|
| 24 | 2 * 2 * 2 * 3 |
| 36 | 2 * 2 * 3 * 3 |
Общие простые множители: 2 и 3. Умножим их друг на друга:
2 * 3 = 6.
Таким образом, общий делитель чисел 24 и 36 равен 6.
Метод разложения на множители позволяет находить общие делители двух чисел, а также другие числовые закономерности и связи между числами. Этот метод является одним из основных в арифметике и находит широкое применение в решении различных математических задач.
Примеры нахождения наибольшего общего делителя
1. Метод делителей
Метод делителей основан на поиске общих делителей двух чисел. Найдем все делители чисел 24 и 36:
- Делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24
- Делители числа 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Заметим, что наибольший общий делитель двух чисел – это наибольший делитель, который является делителем обоих чисел. Из перечисленных выше делителей, наибольший общий делитель для чисел 24 и 36 равен 12.
2. Алгоритм Евклида
Алгоритм Евклида определяет НОД двух чисел путем последовательного вычитания одного числа из другого до тех пор, пока не будет достигнуто равенство.
Применим алгоритм Евклида для нахождения НОД чисел 24 и 36:
| Шаг | Делимое | Делитель | Остаток |
| 1 | 36 | 24 | 12 |
| 2 | 24 | 12 | 0 |
3. Метод простых чисел
Метод простых чисел основан на разложении двух чисел на их простые множители и нахождении общих простых множителей.
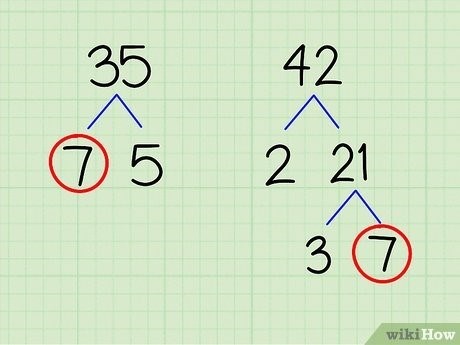
Разложим числа 24 и 36 на простые множители:
- Разложение числа 24 на простые множители: 2 * 2 * 2 * 3 = 2 3 * 3
- Разложение числа 36 на простые множители: 2 * 2 * 3 * 3 = 2 2 * 3 2
Общие простые множители двух чисел – это пересечение множеств простых множителей. Из указанных выше разложений видно, что НОД чисел 24 и 36 равен 2 * 2 * 3 = 12.
В заключении, методы нахождения НОД могут различаться, но результат всегда будет один и тот же. Знание этих методов поможет вам более эффективно решать задачи, связанные с поиском НОД двух чисел.
Как можно это использовать?
В простой и понятной форме рассмотрим, как можно использовать знание о нахождении общего делителя двух чисел в различных ситуациях.
1. Разложение чисел на простые множители
Один из главных способов применения знания о нахождении общего делителя – разложение чисел на простые множители. Это очень полезно, так как такое разложение позволяет увидеть все простые делители числа и оценить его структуру.
2. Упрощение дробей
Другим важным применением общего делителя является упрощение дробей. Если в числителе и знаменателе дроби есть общий делитель, то его можно сократить, получив более простую и удобную форму записи. Например: 16/24 можно сократить на общий делитель 8, получив 2/3.
3. Нахождение наименьшего общего делителя (НОД)
Знание о нахождении общего делителя также применяется для нахождения наименьшего общего делителя (НОД) двух или более чисел. НОД – это наименьшее число, которое делится без остатка на все указанные числа. Например, для чисел 24 и 36, НОД будет равен 12.
4. Решение уравнений и задач
Методы нахождения общего делителя могут быть использованы для решения уравнений и задач различной сложности. Например, при решении задачи, связанной с распределением продуктов на равные части между людьми, знание общего делителя будет ключевым фактором для определения возможных вариантов разделения.
5. Криптография и безопасность данных
Общие делители также используются в криптографии и системах безопасности данных. Например, в алгоритме RSA для шифрования и дешифрования информации используется знание о нахождении общего делителя.
Как видно из приведенных примеров, знание о нахождении общего делителя двух чисел является важным и приложимым в различных областях. Навык нахождения и использования общего делителя поможет в решении математических задач, анализе числовых структур и обеспечении безопасности данных.

Об этой статье
В данной статье мы рассмотрим методы нахождения общего делителя двух чисел, а также приведем примеры их применения. Обладая достаточными знаниями и навыками, вы сможете легко находить общий делитель двух чисел и использовать это знание в различных сферах своей жизни.
Методы нахождения общего делителя
Существует несколько методов нахождения общего делителя двух чисел. Они могут быть применены как вручную, так и при помощи программных средств.
- Метод наименьшего общего делителя (НОД): данный метод основывается на поиске наименьшего числа, на которое делятся оба числа без остатка. Путем последовательного деления можно найти НОД чисел.
- Метод Эвклида: данный метод основывается на поиске НОД чисел с помощью вычитания. Он эффективен и быстро находит общий делитель.
Примеры применения
Нахождение общего делителя может быть полезно в различных сферах жизни:
- Математика: при решении задач, связанных с дробями, факторизацией чисел и другими математическими операциями.
- Криптография: в криптографических алгоритмах требуется нахождение общего делителя для шифрования и расшифрования данных.
- Финансы: в финансовых расчетах, связанных с валютными операциями и процентными ставками, нахождение общего делителя может быть полезным.
- Наука и исследования: в различных областях науки может потребоваться нахождение общего делителя для анализа данных и разработки моделей.
Нахождение общего делителя двух чисел является важной задачей, которая может быть решена различными методами. Знание этих методов позволит вам быть более компетентным в решении математических задач, а также применять их в различных сферах жизни, где требуется нахождение общего делителя.
Бинарный метод поиска НОД
- Для двух чисел a и b, где a > b, если b делит a без остатка, то НОД(a, b) = b.
- Если b не делит a без остатка, то НОД(a, b) = НОД(b, a % b), где % обозначает операцию взятия остатка от деления.
- Процесс повторяется, пока b не станет равным 0.
Бинарный метод поиска НОД можно представить в виде следующего алгоритма:
- Проверить, является ли одно из чисел a или b равным 0. Если да, то НОД(a, b) = max(a, b).
- Проверить, являются ли числа a и b четными. Если да, то НОД(a, b) = 2 * НОД(a/2, b/2).
- Проверить, является ли a четным и b нечетным, или наоборот. Если да, то НОД(a, b) = НОД(a/2, b) (если a четное и b нечетное) или НОД(a, b/2) (если a нечетное и b четное).
- Если a и b нечетные, то НОД(a, b) = НОД((a-b)/2, b) (если a > b) или НОД(a, (b-a)/2) (если b > a).
Преимущества использования бинарного метода поиска НОД:
- Эффективность: благодаря разложению чисел в бинарную форму, алгоритм выполняется очень быстро.
- Универсальность: метод подходит для поиска НОД любых целых чисел.
- Простота: алгоритм достаточно просто реализовать и понять.
Бинарный метод поиска НОД является одним из наиболее эффективных алгоритмов для нахождения НОД двух чисел. Он основывается на использовании бинарного разложения чисел и позволяет найти НОД в очень короткое время. Важно отметить, что этот метод может быть использован для нахождения НОД любых целых чисел, что делает его универсальным инструментом.
Алгоритм Евклида для нахождения НОД
Для нахождения наибольшего общего делителя (НОД) двух чисел существует эффективный алгоритм, который называется алгоритмом Евклида. Этот алгоритм основан на простом принципе вычитания одного числа из другого, пока не будет достигнуто нулевое значение одного из чисел.
Шаги алгоритма Евклида:
- Выберите два числа, для которых необходимо найти НОД.
- Разделите большее число на меньшее число и запишите остаток от деления.
- Если остаток равен нулю, то меньшее число является НОД.
- Если остаток не равен нулю, замените большее число на меньшее число, меньшее число на остаток и повторите шаг 2.
- Повторяйте шаги 2-4, пока не будет найден НОД.
Пример алгоритма Евклида:
Пусть необходимо найти НОД для чисел 48 и 36.
| Шаг | Большее число | Меньшее число | Остаток |
|---|---|---|---|
| 1 | 48 | 36 | |
| 2 | 36 | 12 | 0 |
Итак, НОД для чисел 48 и 36 равен 12.

Важные свойства алгоритма Евклида:
- Алгоритм всегда завершает свою работу после конечного числа шагов.
- Алгоритм не зависит от порядка выбора чисел.
Алгоритм Евклида является одним из основных и наиболее эффективных методов для нахождения НОД двух чисел. Он широко применяется в математике, информатике и других областях, где требуется работа с делимостью и нахождением общих делителей.
Как найти НОД?
Существует несколько способов найти НОД двух чисел:
1. Метод деления
Метод деления является основным способом нахождения НОД. Он основан на следующем принципе: для двух чисел a и b НОД(a, b) равен НОД(b, a mod b), где a mod b – это остаток от деления a на b.
| Число a | Число b | Остаток от деления a на b |
|---|---|---|
| 24 | 18 | 6 |
| 18 | 6 | 0 |
Поэтапно повторяем деление до тех пор, пока не получим остаток 0. НОД будет равен последнему ненулевому остатку.
2. Метод простых чисел
Метод простых чисел заключается в разложении каждого числа на простые множители и нахождении их общих простых множителей. После этого НОД будет равен произведению общих простых множителей.
Например, для чисел 24 и 18:
- Число 24 разложим на простые множители: 2 * 2 * 2 * 3 = 2 3 * 3.
- Число 18 разложим на простые множители: 2 * 3 * 3 = 2 * 3 2.
- Общие простые множители: 2 и 3.
- НОД(24, 18) = 2 * 3 = 6.
В итоге, НОД равен 6.
Найти НОД двух чисел можно различными методами, однако метод деления и метод простых чисел являются наиболее распространенными и эффективными способами.
Что мы узнали?
Общий делитель
Общий делитель двух чисел – это число, которое делит оба числа без остатка. Важно уметь находить общий делитель, так как он может использоваться для упрощения дробей или нахождения наименьшего общего кратного.
Алгоритм Евклида
Алгоритм Евклида является эффективным способом нахождения общего делителя двух чисел. Он основан на последовательном нахождении остатка при делении одного числа на другое до тех пор, пока остаток не станет равным нулю. Получившийся в этот момент делитель и будет являться общим делителем входных чисел.

Наибольший общий делитель (НОД)
Наибольший общий делитель двух чисел – это наибольшее число, которое делит оба числа. Он может быть найден с помощью алгоритма Евклида. НОД используется для упрощения дробей и других математических операций.
Связь общего делителя с простыми числами
Общий делитель двух чисел может быть разложен на простые множители. Для нахождения всех общих делителей, необходимо найти все простые множители каждого из чисел и взять их общие элементы. Таким образом, можно найти все общие делители и наибольший общий делитель двух чисел.
Таблица. Пример нахождения общих делителей
| Число A | Число B | Общие делители |
|---|---|---|
| 12 | 18 | 1, 2, 3, 6 |
| 24 | 36 | 1, 2, 3, 4, 6, 12 |
| 8 | 12 | 1, 2, 4 |
Таким образом, в ходе изучения темы мы узнали, что общий делитель двух чисел можно находить с помощью алгоритма Евклида, что наибольший общий делитель является наибольшим общим делителем этих чисел, а также как связан общий делитель с простыми множителями. Такая информация может быть полезной при решении различных математических задач и проблем.
Урок 6: Наибольший общий делитель. Алгоритм Евклида
Алгоритм Евклида может быть легко реализован с помощью программирования и обеспечивает точный и эффективный способ нахождения наибольшего общего делителя двух чисел. Этот алгоритм также имеет множество практических применений, например, в криптографии и математике.
В ходе урока мы рассмотрели несколько примеров применения алгоритма Евклида для нахождения наибольшего общего делителя. Мы также обсудили расширенный алгоритм Евклида, который позволяет находить коэффициенты Безу, удовлетворяющие линейному уравнению ax + by = gcd(a, b).
В результате изучения алгоритма Евклида мы теперь обладаем мощным инструментом для нахождения наибольшего общего делителя двух чисел. Этот инструмент может быть полезен во многих областях, где требуется работа с делимостью чисел. Урок 6 завершен, и мы готовы применить полученные знания на практике!