Наименьший общий знаменатель (НОЗ) – это самое маленькое число, на которое делятся два или более числа. Нахождение НОЗ является важным шагом во многих математических задачах, особенно при работе с дробями. В этой статье мы рассмотрим несколько методов поиска НОЗ и дадим примеры их применения.
Наименьший общий знаменатель: основные понятия и методы нахождения
Существует несколько методов для нахождения НОЗ. Вот некоторые из них:
Метод нахождения НОЗ через простые множители
Для нахождения НОЗ через простые множители необходимо выполнить следующие шаги:
- Разложить каждое число на простые множители.
- Взять все простые множители с максимальной степенью.
- Умножить эти множители.
Результат будет являться НОЗ заданных чисел.

Метод нахождения НОЗ через факторизацию
Факторизация – это разложение числа на простые множители. Для нахождения НОЗ через факторизацию нужно:
- Факторизовать каждое число.
- Выбрать все различные простые множители с максимальной степенью.
- Умножить эти множители.
Таким образом получим НОЗ заданных чисел.
Пример
Допустим, нам необходимо найти НОЗ чисел 15 и 20.
Разложим числа на простые множители:
- 15 = 3 * 5
- 20 = 2 2 * 5
Возьмем все простые множители с максимальной степенью и умножим их:
НОЗ(15, 20) = 2 2 * 3 * 5 = 60
Таким образом, НОЗ чисел 15 и 20 равен 60.
Наименьший общий знаменатель является важным понятием в математике. Нахождение НОЗ позволяет проводить различные операции с дробями и другими математическими выражениями. Методы нахождения НОЗ через простые множители и факторизацию позволяют эффективно находить НОЗ заданных чисел.
Примеры для закрепления теории
Для лучшего понимания принципов нахождения наименьшего общего знаменателя (НОЗ) в математике, рассмотрим некоторые примеры:

Пример 1: Нахождение НОЗ для двух чисел
Пусть нам требуется найти НОЗ для чисел 12 и 15.
1. Представим числа в виде простых множителей:
- 12 = 2 * 2 * 3
- 15 = 3 * 5
2. Найдем максимальные показатели простых множителей:
- 2 встречается в числе 12 один раз, а в числе 15 отсутствует
- 3 встречается в обоих числах один раз
- 5 встречается в числе 15 один раз, а в числе 12 отсутствует
3. Умножаем простые множители на максимальные показатели:
- 2 * 2 * 3 * 5 = 60
Значит, НОЗ для чисел 12 и 15 равен 60.
Пример 2: Нахождение НОЗ для трех чисел
Рассмотрим числа 6, 8 и 12.
1. Представим числа в виде простых множителей:
- 6 = 2 * 3
- 8 = 2 * 2 * 2
- 12 = 2 * 2 * 3
2. Найдем максимальные показатели простых множителей:
- 2 встречается во всех трех числах максимальное количество раз – три раза
- 3 встречается в числах 6 и 12 максимальное количество раз – один раз
3. Умножаем простые множители на максимальные показатели:

- 2 * 2 * 2 * 3 = 24
Таким образом, НОЗ для чисел 6, 8 и 12 равен 24.
Пример 3: Нахождение НОЗ для дробей
Рассмотрим дроби 1/4, 3/8 и 7/12.
1. Представим дроби в виде общего знаменателя:
- 1/4 = 3/12
- 3/8 = 3/12
- 7/12
2. Найдем наименьший общий знаменатель: 12
Таким образом, НОЗ для дробей 1/4, 3/8 и 7/12 равен 12.
Правила алгоритма для приведения дробей к общему знаменателю
Шаг 1: Найдите наименьшее общее кратное (НОК) знаменателей
Первым шагом в алгоритме приведения дробей к общему знаменателю является нахождение наименьшего общего кратного (НОК) их знаменателей. НОК может быть найден путем разложения знаменателей на простые множители и выбора их общих множителей с наибольшими показателями.
Пример:
Для дробей 3/4 и 2/3, знаменатели 4 и 3 могут быть разложены на простые множители: 4 = 2 * 2 и 3 = 3. Общие множители: 2 и 3. НОК = 2 * 2 * 3 = 12.
Шаг 2: Приведите каждую дробь к общему знаменателю
Вторым шагом является приведение каждой дроби к общему знаменателю путем умножения числителя и знаменателя на фактор, равный отношению НОК к исходному знаменателю.
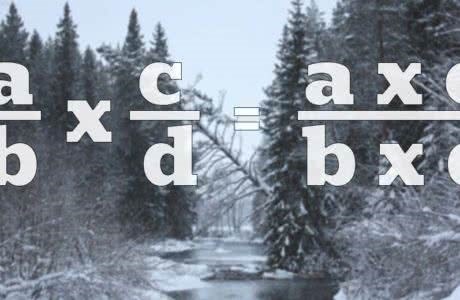
Пример:
Для дроби 3/4 и общего знаменателя 12, фактор приведения равен 12/4 = 3. Приведенная дробь становится 3 * 3/4 * 3 = 9/12.
Шаг 3: Выполните необходимые операции
После приведения дробей к общему знаменателю можно выполнять различные операции с ними, такие как сложение, вычитание, умножение и деление. Для сложения или вычитания, числители складываются или вычитаются, а знаменатели остаются неизменными.
Пример:
Для дробей 9/12 и 2/12, соответственно, результатом сложения будет 9/12 + 2/12 = 11/12.
Итоги
Алгоритм приведения дробей к общему знаменателю включает в себя нахождение НОК знаменателей, приведение каждой дроби к общему знаменателю и выполнение необходимых операций. При соблюдении данных правил, мы можем эффективно работать с дробями и получать точные результаты.
Общий знаменатель для нескольких дробей
Как найти общий знаменатель для нескольких дробей?
Существует несколько методов нахождения общего знаменателя для нескольких дробей:
- Метод наименьших общих кратных (НОК).
НОК двух чисел можно найти с помощью их простого разложения на множители и выбора наибольшего общего множителя. После нахождения НОК двух чисел, можно последовательно находить НОК с другими числами, пока не будет найден общий знаменатель. - Метод сравнения знаменателей.
Если знаменатели дробей уже имеют общий делитель, то этот делитель является их общим знаменателем. Если нет общих делителей, можно применить метод поиска наименьшего общего кратного (НОК). - Метод преобразования в десятичные дроби.
Если мы преобразуем все дроби в десятичные дроби, то можем найти общий знаменатель, если у всех дробей будет один и тот же знаменатель в десятичной форме. Однако этот метод может потребовать дополнительных вычислений и не всегда является эффективным.
Зачем нам нужен общий знаменатель?
Нахождение общего знаменателя для нескольких дробей позволяет нам выполнять операции со сложением или вычитанием этих дробей. Используя общий знаменатель, мы можем привести все дроби к одному и тому же знаменателю и легче проводить с ними арифметические операции.
Пример:

Пусть у нас есть дроби 1/6 и 1/3. Найдем общий знаменатель для этих двух дробей:
- Метод наименьших общих кратных (НОК).
Простое разложение чисел: 6 = 2 * 3, 3 = 3. НОК: 2 * 3 = 6. Общий знаменатель: 6. - Метод сравнения знаменателей.
Знаменатели уже имеют общий делитель (6), поэтому 6 является их общим знаменателем. - Метод преобразования в десятичные дроби.
Десятичные представления дробей: 1/6 = 0.1666…, 1/3 = 0.3333… Общий знаменатель: 10.
Таким образом, общий знаменатель для дробей 1/6 и 1/3 равен 6.
Что такое НОК и как его найти
Наименьшим общим кратным (НОК) двух или более чисел называется наименьшее число, которое делится на каждое из этих чисел без остатка.
Для нахождения НОК двух чисел можно использовать различные методы, но наиболее распространенным является метод разложения чисел на простые множители.
Процесс нахождения НОК с помощью метода разложения чисел на простые множители выглядит следующим образом:
- Разложить каждое число на простые множители.
- Взять все простые множители с наибольшей степенью.
- Множественное все простые множители с наибольшей степенью.
Найденное таким образом число и будет являться НОК исходных чисел.
НОК является важным понятием в математике и широко используется при решении различных задач, связанных с работой с дробями, периодами и т.д.
Таким образом, НОК позволяет найти наименьшее общее кратное двух или более чисел и упрощает дальнейшие вычисления и анализ.