Исследование функций с помощью производной – это метод анализа, который позволяет определить характеристики функции, такие как экстремумы, точки перегиба и монотонность. Для этого используется производная функции, которая показывает ее скорость изменения в каждой точке. Исследование функций позволяет лучше понять их поведение и удобно применяется в различных областях математики и физики.
Полный пример решения онлайн
В настоящее время существует множество онлайн-сервисов и программ, которые позволяют решать математические задачи, в том числе исследование функций с помощью производной. Рассмотрим полный пример решения подобной задачи с использованием одного из таких сервисов.
Шаг 1: Ввод исходных данных
Первым этапом в решении задачи исследования функции с помощью производной является ввод исходных данных. В нашем примере предположим, что дана функция f(x) = x 2 – 3x + 2. Для ее исследования построим график и найдем ее производную.
Шаг 2: Построение графика функции
Следующим шагом будет построение графика функции f(x). Для этого воспользуемся графическим редактором, доступным в онлайн-сервисе. Результатом будет график функции, который позволит наглядно оценить ее поведение и установить основные точки перегиба, экстремумы и разрывы.
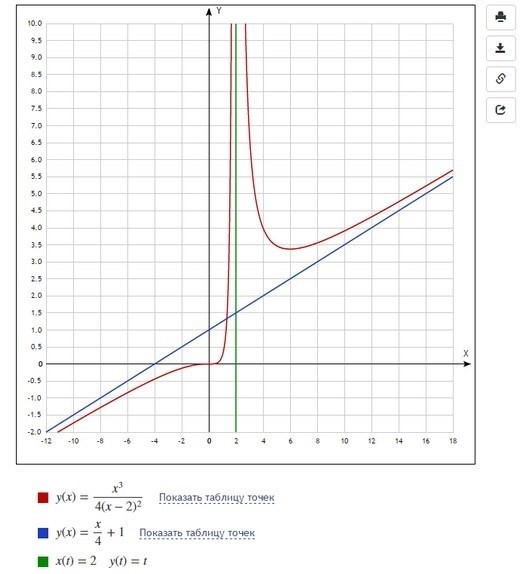
График функции f(x) = x 2 – 3x + 2:
| x | f(x) |
|---|---|
| 0 | 2 |
| 1 | 0 |
| 2 | 0 |
| 3 | 2 |
Шаг 3: Нахождение производной функции
После построения графика функции, перейдем к нахождению ее производной. Воспользуемся онлайн-калькулятором для нахождения производной функции f(x). Производная позволяет определить значения тангенса угла наклона касательной к графику функции в каждой точке исследования.
Производная функции f(x) = x 2 – 3x + 2:
| x | f'(x) |
|---|---|
| 0 | -3 |
| 1 | -2 |
| 2 | 1 |
| 3 | 4 |
Шаг 4: Анализ полученных результатов
Имея на руках график функции и значения производной, можно провести анализ поведения функции. Интерпретируя результаты можно, например, определить точки экстремумов, изучить поведение функции при удалении от центра на интервалах между экстремумами, определить наличие и расположение точек перегиба.
Анализ:
- Точка (1, 0) является локальным минимумом.
- Точка (2, 0) является точкой перегиба.
- Точка (3, 2) является локальным максимумом.
Таким образом, проведя исследование функции f(x) = x 2 – 3x + 2 с помощью производной, мы получили информацию о ее поведении и определили основные характеристики функции.
Общая схема исследования
1. Определение области определения функции
Первым шагом является определение области определения функции, то есть множества всех возможных значений аргумента функции. Область определения функции может быть ограничена или неограничена.
2. Вычисление производной функции
Далее необходимо вычислить производную функции. Производная функции показывает, как меняется значение функции с изменением аргумента. Существуют различные методы вычисления производной, включая правила дифференцирования и применение формул. Полученная производная может быть аналитической или численной.
3. Анализ монотонности и экстремумов
После вычисления производной функции следует анализировать ее монотонность и нахождение экстремумов (минимумы и максимумы). Для этого необходимо находить интервалы возрастания и убывания функции, а также точки экстремума, в которых производная равна нулю или не существует.
4. Исследование выпуклости и вогнутости
Далее проводится исследование функции на выпуклость и вогнутость. Для этого анализируются вторые производные функции. Если вторая производная положительна на интервале, то функция является выпуклой. Если вторая производная отрицательна на интервале, то функция является вогнутой.
5. Построение графика функции
И последним шагом исследования является построение графика функции на основе полученных данных. График позволяет визуализировать поведение функции и наглядно представить ее свойства и характеристики.
Больше знаний: теория и практика
Теория: изучение основных понятий и методов
Для начала исследования функции с помощью производной необходимо обладать фундаментальными знаниями о производной и ее свойствах. Мы изучаем понятие производной, формулы для нахождения производной различных функций, правила дифференцирования, а также методы определения экстремумов и перегибов функции.
- Изучаем уравнения касательных и нормалей;
- Определяем точки экстремумов и исследуем их поведение;
- Анализируем перегибы функции и их характеристики.
Изучение теории помогает нам уяснить основные понятия и научиться применять методы дифференцирования для определения исследуемых характеристик функции.
Практика: применение полученных знаний в реальных задачах
- Решаем задачи оптимизации, находя максимумы и минимумы функций при определенных условиях;
- Анализируем поведение функций в окрестности точек экстремумов и перегибов;
- Строим графики функций и исследуем их особенности.
Практическое применение позволяет нам проверить и углубить наши теоретические знания, а также развивает навыки анализа и решения задач.
Исследование функций с помощью производной представляет собой сочетание теоретического и практического подходов к изучению предмета. Такой подход позволяет получить полное и глубокое понимание функциональных зависимостей и развить навыки анализа и решения задач. Больше знаний – больше возможностей!
Наибольшее и наименьшее значение функции
Исследование функции с помощью производной позволяет определить наибольшее и наименьшее значение функции. Это важная информация для анализа поведения функции и поиска экстремумов.
Наибольшее значение функции называется максимумом, а наименьшее – минимумом. Обычно нахождение этих значений является одной из ключевых задач при исследовании функций.
Нахождение максимума и минимума функции
Для нахождения максимума и минимума функции необходимо:
- Найти все критические точки функции, то есть точки, в которых производная равна нулю или не существует.
- Дополнительно проверить значения функции в крайних точках области определения функции.
- Сравнить значения функции в найденных точках и выбрать наибольшее и наименьшее значение.
Пример
Рассмотрим функцию f(x) = x 2 – 4x + 3 и найдем ее максимум и минимум.
1. Найдем критические точки, приравняв производную функции к нулю:
f'(x) = 2x – 4 = 0
2. Решим уравнение:
| x | f'(x) |
|---|---|
| 2 | 0 |
Критическая точка функции – x = 2.
3. Проверим значения функции в крайних точках области определения функции:
| x | f(x) |
|---|---|
| 0 | 3 |
| 3 | 0 |
4. Сравним значения функции в найденных точках:
| Точка | Значение функции |
|---|---|
| x = 0 | f(0) = 3 |
| x = 2 | f(2) = -1 |
| x = 3 | f(3) = 0 |
Минимум функции – f(2) = -1, максимум функции – f(0) = 3.
Таким образом, минимум функции f(x) = x 2 – 4x + 3 равен -1, а максимум равен 3.
Производные основных функций
Основные функции, включающиеся в исследование, включают в себя:
1. Линейная функция
Линейная функция имеет вид y = kx + b, где k и b – постоянные коэффициенты. Производная линейной функции равна коэффициенту k, что означает, что скорость изменения функции в каждой точке равна k.
2. Квадратичная функция
Квадратичная функция имеет вид y = ax 2 + bx + c, где a, b и c – постоянные коэффициенты. Производная квадратичной функции представляет собой линейную функцию, которая показывает скорость изменения функции в каждой точке.
3. Показательная функция
Показательная функция имеет вид y = a x, где a – постоянное число. Производная показательной функции равна ее значению в данной точке, умноженному на натуральный логарифм основания a.
4. Логарифмическая функция
Логарифмическая функция имеет вид y = log_a(x), где a – постоянное число. Производная логарифмической функции равна 1, деленная на произведение значения функции и натурального логарифма основания a.
5. Синусоидальная функция
Синусоидальная функция имеет вид y = a*sin(bx + c), где a, b и c – постоянные коэффициенты. Производная синусоидальной функции равна произведению значения функции на коэффициент b.
6. Косинусоидальная функция
Косинусоидальная функция имеет вид y = a*cos(bx + c), где a, b и c – постоянные коэффициенты. Производная косинусоидальной функции равна произведению значения функции на коэффициент -b.
7. Полиномиальная функция
Полиномиальная функция имеет вид y = a_n*x n + a_(n-1)*x (n-1) + … + a_1*x + a_0, где a_0, a_1, …, a_n – постоянные коэффициенты. Производная полиномиальной функции является суммой произведений каждого члена функции на его степень.
8. Рациональная функция
Рациональная функция имеет вид y = (P(x)) / (Q(x)), где P(x) и Q(x) – полиномиальные функции. Производная рациональной функции выражается через производные этих полиномиальных функций.
| Функция | Производная |
|---|---|
| y = 3x | dy/dx = 3 |
| y = 2x 2 | dy/dx = 4x |
| y = e x | dy/dx = e x |
| y = ln(x) | dy/dx = 1/x |
| y = sin(x) | dy/dx = cos(x) |
| y = cos(x) | dy/dx = -sin(x) |
Исследование функций с помощью производной позволяет более подробно изучить их свойства и поведение в разных точках. Это полезный инструмент при решении задач из различных областей, включая физику, экономику и естественные науки.
Выпуклость и вогнутость функции
Функция называется выпуклой на интервале, если её график на этом интервале лежит выше любой касательной, проведенной к нему. Вогнутая функция, наоборот, имеет график, лежащий ниже любой проведенной к нему касательной. Для определения выпуклости и вогнутости функции используются различные методы, включая анализ производных и вторых производных.
Методы определения выпуклости и вогнутости функции
- Анализ производной: Если производная функции на интервале положительна (или неотрицательна), то функция выпукла на этом интервале. Если производная отрицательна (или не положительна), функция вогнута. Если производная меняет знак, то есть переходит из положительного в отрицательное или наоборот, то функция имеет точку перегиба.
- Анализ второй производной: Если вторая производная положительна (или неотрицательна), то функция выпукла на интервале. Если вторая производная отрицательна (или не положительна), функция вогнута. Точка, где вторая производная обращается в нуль, является кандидатом на точку перегиба.
Свойства выпуклой и вогнутой функции
Выпуклая функция обладает следующими свойствами:
- График функции лежит выше любой касательной.
- Множество значений функции является выпуклым множеством.
- Если функция дважды дифференцируема, то производная возрастает.
Вогнутая функция, в свою очередь, обладает следующими свойствами:
- График функции лежит ниже любой касательной.
- Множество значений функции является вогнутым множеством.
- Если функция дважды дифференцируема, то производная убывает.
Выпуклость и вогнутость функции – это важные свойства, которые помогают анализировать её поведение и определять критические точки. Определение выпуклости и вогнутости функции можно осуществить с помощью анализа производной и второй производной. Изучение данных характеристик функций позволяет более точно описывать их поведение и принимать обоснованные решения в различных областях науки и техники.
Как построить график онлайн?
Шаги для построения графика онлайн:
- Выбор инструмента. Перед тем, как приступить к построению графика, необходимо выбрать подходящий онлайн-ресурс или программу. Важно учитывать функциональность инструмента, возможности настройки внешнего вида графика, а также доступность различных типов графиков.
- Ввод данных. После выбора инструмента необходимо ввести данные, на основе которых будет строиться график. Данные могут быть представлены в виде числовых значений или в формате таблицы.
- Выбор типа графика. В зависимости от цели и задач, необходимо выбрать подходящий тип графика. Это может быть линейный график, столбчатая диаграмма, круговая диаграмма и другие. Каждый тип графика имеет свои особенности и предназначен для визуализации определенных данных.
- Настройка графика. После выбора типа графика можно настроить его внешний вид. Некоторые инструменты позволяют изменять цвета, подписи осей, добавлять заголовки и легенду для более точного представления данных.
Преимущества построения графика онлайн:
- Быстрота и удобство. Онлайн-инструменты позволяют построить график всего за несколько кликов. Не требуется установка дополнительного программного обеспечения.
- Интерактивность. Некоторые онлайн-ресурсы позволяют взаимодействовать с графиком, изменять параметры и отображать подробную информацию по каждой точке на графике.
- Визуализация данных. График помогает наглядно представить данные, выявить зависимости и тренды, что упрощает анализ и принятие решений.
- Доступность и широкий выбор. Онлайн-инструменты доступны каждому пользователю с доступом в Интернет и предлагают большой выбор типов графиков для различных целей и задач.
Построение графика онлайн – удобный и эффективный способ визуализации данных. Этот инструмент помогает увидеть связи и зависимости между различными параметрами, а также предоставляет возможность анализировать данные и делать информированные решения.
Примеры решений по исследованию функции
Рассмотрим несколько примеров решений задач по исследованию функции с помощью производной.
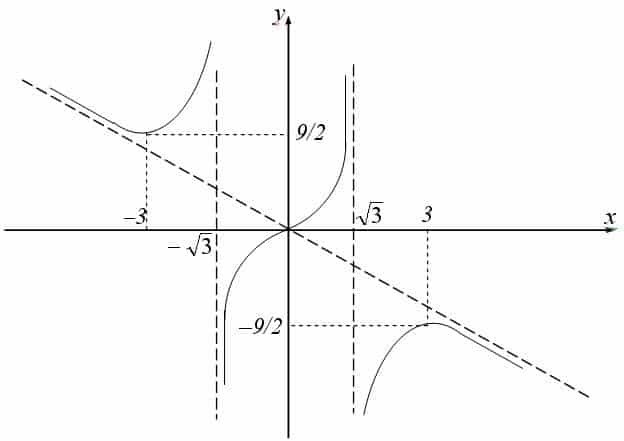
Пример 1:
Исследуем функцию f(x) = x 2 – 3x + 2.
1. Найдем производную функции: f'(x) = 2x – 3.
2. Решим уравнение f'(x) = 0 для нахождения критических точек.
2x – 3 = 0
x = 3/2
3. Выпишем значения исследуемой функции и ее производной в найденных критических точках. Проанализируем знаки производной и ее изменение в окрестности критических точек.
| x | f(x) | f'(x) |
|---|---|---|
| x < 3/2 | + | + |
| x = 3/2 | -1/4 | 0 |
| x > 3/2 | + | + |
4. Определим наличие экстремумов и точек перегиба, а также поведение функции на бесконечностях.
В данном случае у нас есть минимум функции при x = 3/2. Функция убывает на интервале (-∞, 3/2) и возрастает на интервале (3/2, +∞).
Пример 2:
Исследуем функцию f(x) =e x – x 2.
1. Найдем производную функции: f'(x) = e x – 2x.
2. Решим уравнение f'(x) = 0 для нахождения критических точек.

e x – 2x = 0
x ≈ 0.7035
3. Выпишем значения исследуемой функции и ее производной в найденных критических точках. Проанализируем знаки производной и ее изменение в окрестности критических точек.
| x | f(x) | f'(x) |
|---|---|---|
| x < 0.7035 | – | – |
| x ≈ 0.7035 | + | 0 |
| x > 0.7035 | + | + |
4. Определим наличие экстремумов и точек перегиба, а также поведение функции на бесконечностях.
У нас есть максимум функции при x ≈ 0.7035. Функция возрастает на интервале (-∞, 0.7035) и убывает на интервале (0.7035, +∞).
Исследование функций с помощью производной – это мощный инструмент для определения поведения функции, нахождения экстремумов и точек перегиба. При решении задач рекомендуется последовательно выполнять шаги: нахождение производной, решение уравнения на равенство нулю, анализ знаков исследуемой функции и ее производной в критических точках, определение наличия экстремумов и точек перегиба, а также изучение поведения функции на бесконечностях.