Сокращенное умножение – это способ умножения двух множителей, при котором отбрасываются некоторые операции, основываясь на дистрибутивности и свойствах алгебры. В результате сокращенного умножения получаются более компактные и удобные для вычислений выражения.
Существуют несколько основных формул сокращенного умножения, которые широко используются в алгебре:
1. Формула квадрата суммы
Квадрат суммы двух выражений можно выразить с помощью сокращенного умножения:
(а + b) 2 = а 2 + 2ab + b 2.
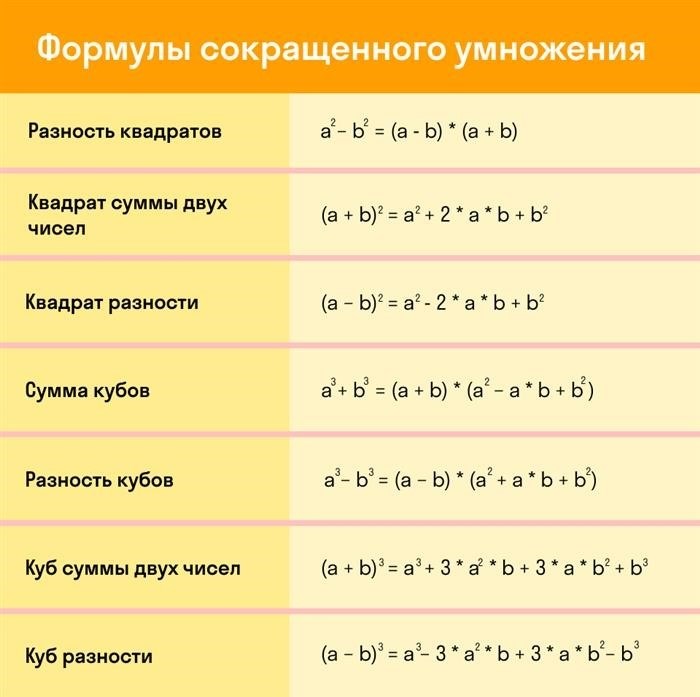
2. Формула квадрата разности
Квадрат разности двух выражений также можно выразить с помощью сокращенного умножения:
(а – b) 2 = а 2 – 2ab + b 2.
3. Формула суммы квадратов
Сумму квадратов двух выражений можно представить с помощью сокращенного умножения:

(а + b)(а – b) = а 2 – b 2.
4. Правило трех частей
Правило трех частей позволяет упростить произведение трех выражений:
(а + b)(а + c)(b + c) = а 2b + а 2c + ab 2 + abc + b 2c + bc 2.
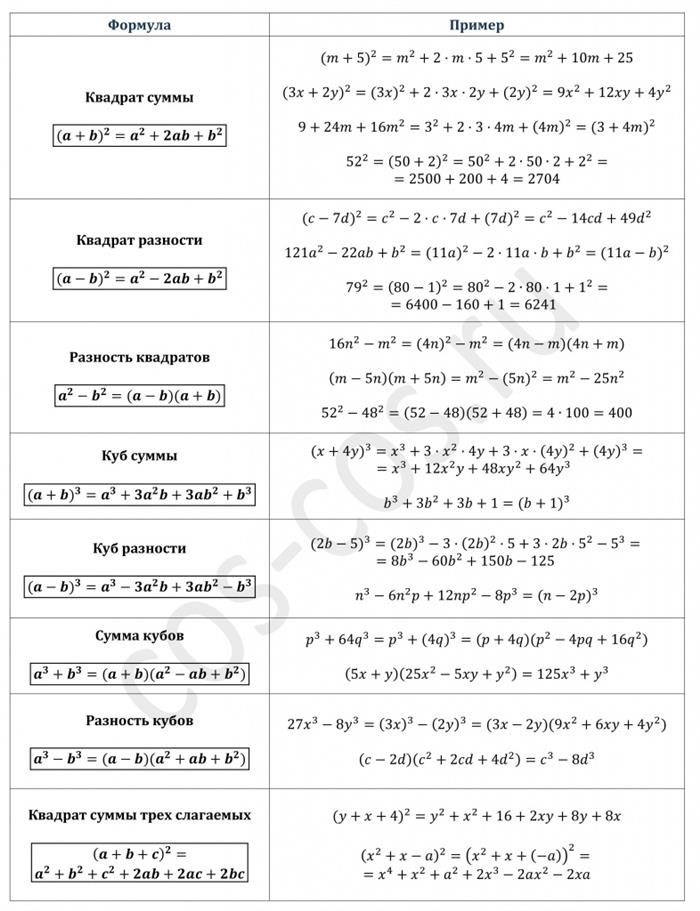
Применение формул сокращенного умножения упрощает процесс вычислений и делает алгебраические выражения более компактными. Эти формулы являются основой для решения многих задач и уравнений в алгебре.
Популярные вопросы и ответы
1. Что такое формулы сокращенного умножения?
Формулы сокращенного умножения в алгебре позволяют упростить запись выражений и умножения чисел или переменных. Они являются компактной формой записи и помогают сократить количество символов в выражении.
2. Какие основные формулы сокращенного умножения существуют?

Наиболее популярными формулами сокращенного умножения являются квадрат суммы двух чисел, квадрат разности двух чисел, квадрат суммы и разности двух чисел, куб суммы и разности двух чисел. Также, существуют формулы сокращенного умножения для бинома Ньютона, которые позволяют раскрыть скобки с высокой степенью.
3. Для чего используются формулы сокращенного умножения?
Формулы сокращенного умножения используются для упрощения записи и решения математических выражений. Они позволяют вычислить результат умножения чисел или переменных, не проводя фактических математических операций и раскрытия скобок. Формулы сокращенного умножения также применяются в различных областях науки, инженерии и физике для упрощения вычислений.

4. Как использовать формулы сокращенного умножения?
Для использования формул сокращенного умножения необходимо знать соответствующую формулу и подставить значения чисел или переменных в нее. Затем нужно выполнить умножение согласно формуле и получить результирующее значение. Формулы сокращенного умножения можно использовать для упрощения выражений, проведения алгебраических преобразований и решения уравнений.
Итог
Формулы сокращенного умножения являются важным инструментом в алгебре и математике в целом. Они помогают упростить запись выражений и выполнить умножение без проведения фактических операций. Знание и использование этих формул позволяет существенно упростить вычисления и решение задач.