При рассмотрении движения тела в физике выделяют два основных вида: прямолинейное и криволинейное. Прямолинейное движение тела характеризуется изменением положения тела только по одной прямой линии, в то время как криволинейное движение тела представляет собой изменение местоположения тела по кривой линии. Особый случай криволинейного движения – движение тела по окружности.
Криволинейное движение по окружности
Основные характеристики криволинейного движения по окружности:
- Тело движется по кривой траектории, которая является окружностью;
- Скорость тела постоянна по модулю, но меняется по направлению;
- Ускорение тела направлено к центру окружности и называется центростремительным ускорением;
- Путь, пройденный телом по окружности, зависит от длины окружности и числа оборотов.
Формулы криволинейного движения по окружности:
Для описания криволинейного движения по окружности используются следующие формулы:
- Длина окружности: l = 2πr, где l – длина окружности, r – радиус окружности;
- Период обращения: T = 2πr/v, где T – период обращения, v – скорость движения;
- Центростремительное ускорение: a = v 2/r, где a – ускорение, v – скорость движения, r – радиус окружности.
Пример:
Пусть тело движется по окружности радиусом 5 метров. Его скорость составляет 10 м/c. Найдем период обращения и центростремительное ускорение.
| Величина | Формула | Результат |
|---|---|---|
| Период обращения (T) | T = 2πr/v | T = 2π*5/10 = π с |
| Центростремительное ускорение (a) | a = v 2/r | a = 10 2/5 = 20 м/c 2 |
Таким образом, период обращения равен π секунды, а центростремительное ускорение равно 20 метров в квадрате в секунду.
Движение по окружности
Определение и особенности движения по окружности
Движение по окружности – это движение, при котором тело движется по траектории, которая представляет собой окружность. Тело вращается вокруг некоторого центра окружности. Некоторые особенности движения по окружности включают постоянную по модулю скорость тела и постоянный радиус окружности.
Связь скорости и радиуса движения
Скорость тела, движущегося по окружности, зависит от радиуса этой окружности. Чем меньше радиус, тем большую скорость необходимо иметь, чтобы пройти по окружности за одно и то же время.
Математическое представление связи скорости и радиуса движения дается формулой: v = ω * r, где v – линейная скорость, ω – угловая скорость, r – радиус окружности.
Угловая скорость и период вращения
Угловая скорость – это физическая величина, определяющая изменение угла поворота за единицу времени. Часто используется понятие периода вращения – время, за которое точка, описывающая окружность, проходит один полный оборот.

Центростремительное ускорение
Центростремительное ускорение – это ускорение, направленное к центру окружности, вызванное изменением направления скорости. Математически представляется формулой: a = (v 2) / r, где a – центростремительное ускорение, v – линейная скорость, r – радиус окружности.
Примеры движения по окружности
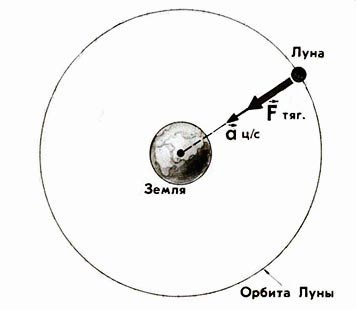
Движение спутника вокруг Земли, вращение электронов в атоме, движение колеса автомобиля по закругленной дороге – все это примеры движения по окружности.

Краткий список особенностей движения по окружности:
- Постоянная по модулю скорость
- Изменение направления движения
- Зависимость скорости от радиуса окружности
- Угловая скорость и период вращения
- Центростремительное ускорение
| Примеры | Описание |
|---|---|
| Движение спутника | Спутник орбитально движется вокруг планеты или другого космического объекта. |
| Вращение электрона | Электрон, находящийся в атоме, вращается вокруг ядра. |
| Движение автомобильного колеса | Колесо автомобиля при движении по закругленной дороге описывает окружность. |
Движение по окружности является одним из фундаментальных типов движения и находит применение в различных сферах науки и техники.

Движение по вертикали
Основные параметры движения по вертикали:
- Высота подъема: максимальное расстояние, которое тело поднимается относительно начальной точки вертикального движения;
- Скорость подъема: скорость, с которой тело перемещается вверх;
- Время подъема: время, затраченное на полный подъем тела;
- Высота падения: максимальное расстояние, на которое тело опускается относительно начальной точки вертикального движения;
- Скорость падения: скорость, с которой тело перемещается вниз;
- Время падения: время, затраченное на полное падение тела;
- Время полета: суммарное время, затраченное на подъем и падение тела.
В случае движения по вертикали, взаимосвязь между вышеперечисленными параметрами определяется законами физики. Например, при падении тела без воздушного сопротивления, время падения будет равно времени подъема, а высота подъема будет равна высоте падения. Если же на тело действует сила сопротивления, то времена подъема и падения будут отличаться, а высоты подъема и падения не будут равными.
Примеры движения по вертикали:
| Тип движения | Характеристики |
|---|---|
| Свободное падение | Тело падает под действием силы тяжести без воздушного сопротивления |
| Подъем по вертикальной трубе | Тело поднимается вверх по вертикальной трубе, поддерживаемое силой, приложенной снизу |
| Бросок вверх | Тело брошено вверх с начальной скоростью |
Итог
В данной статье мы рассмотрели движение тела по окружности с постоянной по модулю скоростью. Отметим следующие важные моменты:

- Тело, движущееся по окружности с постоянной по модулю скоростью, имеет постоянную угловую скорость;
- Угловая скорость выражается через период или частоту вращения;
- Для тела, движущегося по окружности с постоянной по модулю скоростью, характерна равномерная проекция скорости на направление радиуса круга;
- Величина скорости изменяется в зависимости от положения тела на окружности, однако ее модуль остается постоянным;
- Ускорение тела, движущегося по окружности с постоянной по модулю скоростью, направлено к центру окружности и изменяет направление по мере движения по кругу;
- Центростремительное ускорение вычисляется по формуле a = v 2 / R, где v – скорость, R – радиус окружности.
Таким образом, движение тела по окружности с постоянной по модулю скоростью является одним из примеров криволинейного движения и характеризуется равномерным изменением угла и равномерной проекцией скорости. Центростремительное ускорение играет важную роль в таком движении, определяя направление и радиус кривизны окружности.