Деление и умножение обыкновенных дробей являются основными операциями при работе с дробями. Данные операции позволяют упростить выражения с дробями и решить различные математические задачи. В данной статье мы рассмотрим основные правила и алгоритмы для выполнения деления и умножения обыкновенных дробей.
ВОПРОСЫ И ЗАДАНИЯ
В данном разделе представлены вопросы и задания, связанные с делением и умножением обыкновенных дробей. Решение этих задач поможет разобраться в основных принципах работы с дробями и закрепит полученные знания.
Вопросы:
- Что такое обыкновенная дробь?
- Какие шаги следует выполнить при умножении обыкновенных дробей?
- Какими основными свойствами обладает операция умножения дробей?
- Как определить результат деления двух обыкновенных дробей?
- Какими основными свойствами обладает операция деления дробей?
Задания:
Решите следующие задачи:
- Выполните умножение: 2/3 * 4/5.
- Выполните умножение: 3/8 * 5/6.
- Выполните деление: (1/2)/(3/4).
- Выполните деление: (4/5)/(2/3).
- Выполните умножение: (3/4) * (5/6).
Ответы к заданиям:

| Задание | Ответ |
|---|---|
| 1 | 8/15 |
| 2 | 5/16 |
| 3 | 2/3 |
| 4 | 6/5 |
| 5 | 5/8 |
Ознакомьтесь с примерами решений в следующей таблице:
| Задача | Решение |
|---|---|
| На складе имеется 2/3 тонны товара. Сколько тонн товара всего? | Для решения данной задачи необходимо умножить дробь 2/3 на 1 тонну товара. Получаем результат: 2/3 * 1 = 2/3 тонны товара. |
| Дробь 1/2 разделить на дробь 2/3. | Для решения данного задания необходимо выполнить операцию умножения с обратной дробью. Получаем: (1/2) * (3/2) = 3/4. |
Таким образом, решая вопросы и задания, связанные с делением и умножением обыкновенных дробей, вы укрепите свои знания и навыки работы с дробями.
Нахождение дроби от числа
Деление числа на дробь
Деление числа на дробь производится следующим образом:
- Число, которое нужно разделить (делимое), располагается над чертой.
- Дробь, на которую нужно разделить число (делитель), располагается под чертой.
- Производится умножение числа (делимого) на обратную дробь (делитель).
- Полученное произведение является результатом деления числа на дробь.
Полученный результат может быть записан как обыкновенная дробь или десятичная дробь, в зависимости от задачи.
Пример нахождения дроби от числа
Для наглядности рассмотрим пример нахождения дроби от числа:
| Число (делимое) | Дробь (делитель) | Результат деления |
|---|---|---|
| 10 | 1/2 | 5 |
| 12 | 3/4 | 9 |
В первом примере, число 10 делится на дробь 1/2, что равно 5. Во втором примере, число 12 делится на дробь 3/4, что равно 9.
Нахождение дроби от числа включает в себя деление числа на определенное количество частей. При этом используются специальные математические операции, включающие умножение числа на обратную дробь. Полученный результат может быть записан в виде обыкновенной или десятичной дроби, в зависимости от требований задачи.

Об этой статье
В данной статье рассмотрим важную тему деления и умножения обыкновенных дробей. Наше внимание будет акцентировано на разъяснении основных понятий и правил, связанных с этим математическим действием.
Деление обыкновенных дробей
Деление обыкновенных дробей является одним из основных арифметических действий, которые помогают нам решать разнообразные задачи и проблемы. Для правильного деления дробей необходимо следовать определенным правилам:
- Первым шагом необходимо инвертировать делитель, то есть записать его в виде обратной дроби.
- Затем умножаем делимое на инвертированный делитель.
- Полученную дробь можно сократить, если это возможно.
Простые и понятные правила деления обыкновенных дробей позволяют выполнять это действие с легкостью и точностью.
Умножение обыкновенных дробей
Умножение обыкновенных дробей также является важным математическим действием, которое мы используем ежедневно. Для успешного умножения дробей нужно придерживаться следующих правил:
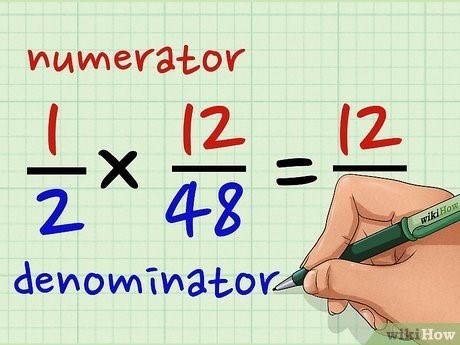
- Перемножаем числители дробей между собой.
- Перемножаем знаменатели дробей между собой.
- Полученные числитель и знаменатель дроби можно сократить, если это возможно.
Знание правил умножения обыкновенных дробей поможет нам решать различные задачи и находить верные ответы.
Примеры задач
Давайте рассмотрим несколько примеров задач, которые помогут нам лучше понять, как применять деление и умножение обыкновенных дробей в повседневной жизни:
- Задача 1: Разделите пирог на 8 равных частей и съешьте 3 части. Какую часть пирога вы съели?
- Задача 2: Если при умножении 5/6 на X мы получили 5/8, какое значение должно быть у X?
- Задача 3: При делении 3/4 на Y мы получили 2/3. Какое значение должно быть у Y?
Решая данные задачи, мы применяем правила деления и умножения обыкновенных дробей и находим верные ответы.

Правильное понимание и применение правил деления и умножения обыкновенных дробей является неотъемлемой частью успешного выполнения математических операций. Глубокое знание данных правил поможет нам решать различные задачи и достигать точных результатов.
Сокращение дробей «на лету»
Сокращение дробей «на лету» – это процесс упрощения дроби до несократимого вида во время выполнения вычислений. Этот метод позволяет быстро получить результат с меньшими значениями числителя и знаменателя, что упрощает дальнейшие математические операции.
Как сократить дробь «на лету»?
- Определите наибольший общий делитель (НОД) числителя и знаменателя дроби.
- Разделите числитель и знаменатель на полученный НОД.
- Получившаяся дробь будет сокращенной.
Пример сокращения дроби «на лету»
| Исходная дробь | Сокращенная дробь |
|---|---|
| 24/36 | 2/3 |
Преимущества сокращения дробей «на лету»
- Экономия времени: сокращение дробей во время вычислений позволяет получить более простой результат без дополнительных шагов.
- Удобство в дальнейших операциях: работа с сокращенными дробями упрощает выполнение математических операций, таких как сложение, вычитание или сравнение.
- Простота восприятия: сокращенные дроби более компактны и понятны для восприятия, особенно при работе с большими или сложными выражениями.
Сокращение дробей «на лету» – эффективный метод, который позволяет упростить вычисления и получить более удобные и компактные результаты. Знание этой техники поможет вам сконцентрироваться на сути математических задач и сделает работу с дробями более легкой и быстрой.
Нахождение числа по заданному значению его дроби
Шаги для нахождения числа по заданной дроби:
- Убедитесь, что дробь задана корректно и имеет числитель и знаменатель.
- Приведите дробь к несократимому виду, если это необходимо, сокращая числитель и знаменатель на их общие множители.
- Определите значение числителя и знаменателя заданной дроби.
- Воспользуйтесь формулой для нахождения числа по заданной дроби:
Число = Числитель / Знаменатель
Пример:
Пусть задана дробь 3/4. Необходимо найти число, которому она соответствует.
Шаг 1:
Дробь 3/4 задана корректно и имеет числитель (3) и знаменатель (4).
Шаг 2:
Данная дробь уже находится в несократимом виде.
Шаг 3:
Числитель заданной дроби равен 3, а знаменатель равен 4.
Шаг 4:
Используем формулу:
Число = 3 / 4
Решим эту формулу:
| Деление | Результат |
|---|---|
| 3 / 4 | 0.75 |
Таким образом, число, которому соответствует дробь 3/4, равно 0.75.
Умножение дробей с целой частью и отрицательных дробей
Умножение дробей с целой частью
Для умножения дроби с целой частью на другую дробь необходимо выполнить следующие шаги:
- Разложить дробь с целой частью на произведение целой части и дроби.
- Умножить каждую из дробей по обычным правилам умножения.
- Сложить полученные произведения.
Например, для умножения дроби 3½ на дробь 2¾:
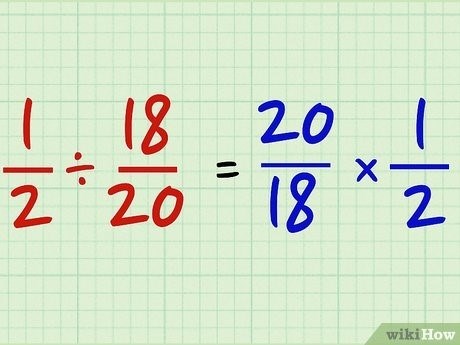
| Шаг | Выполнение |
|---|---|
| 1 | 3½ = 3 + ½ |
| 2 | (3 + ½) * 2¾ = 3 * 2¾ + ½ * 2¾ |
| 3 | 6¾ + 1½ = 8¼ |
Умножение отрицательных дробей
Умножение отрицательных дробей происходит аналогично умножению положительных дробей, с учетом правил умножения отрицательных чисел.
При умножении отрицательных дробей, результат будет положительным число, если количество отрицательных дробей четное. В противном случае, результат будет отрицательным числом.
Например, для умножения дробей -¾ и -½:
| Выполнение | Результат |
|---|---|
| (-¾) * (-½) | ⅜ |
Умножение дробей с целой частью и отрицательных дробей несет важную математическую информацию и помогает в решении различных математических задач. Знание особенностей этой операции позволяет эффективно использовать ее в повседневной жизни и на практике.
Дроби – коротко о главном
Мы разобрали основные шаги деления и умножения дробей: сокращение, приведение к общему знаменателю, умножение числителя и знаменателя и т.д. Освоив эти методы, вы сможете легко выполнять арифметические операции с обыкновенными дробями.
Надеемся, что данная статья помогла вам уяснить принципы деления и умножения обыкновенных дробей. Помните, что практика играет важную роль в освоении математических навыков, поэтому регулярное выполнение упражнений и задач позволит вам стать опытным и уверенным в работе с дробями.