e – это одно из самых важных математических чисел, которое имеет множество интересных свойств. Оно является основанием натурального логарифма и часто встречается в различных областях науки. Е было введено Леонардом Эйлером в 18 веке и с тех пор нашло свое применение в решении широкого спектра задач, от описания экспоненциального роста до решения дифференциальных уравнений.
Смысл числа e
e = 1 + 1/1! + 1/2! + 1/3! + …
Несмотря на начальную простоту этого числа, оно обладает рядом фундаментальных свойств, которые делают его незаменимым в различных областях математики, физики и других наук.
Происхождение
Число e было введено и определено швейцарским математиком Леонардом Эйлером в 18 веке. Буква “e” стала обозначением этой константы в честь французского математика Жака Бернулли, который использовал её в своих работах. Первоначально Эйлер определил число e как предел числовой последовательности в результате бесконечно малых величин.
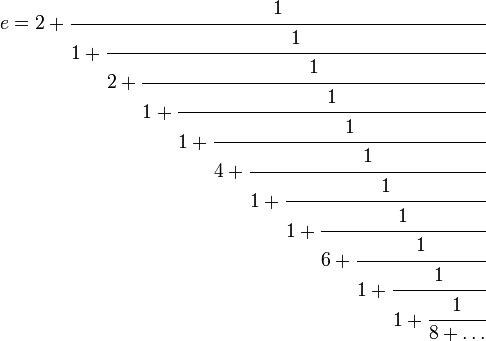
Значение и свойства
Число e является иррациональным и трансцендентным, что означает, что оно не может быть представлено в виде десятичной дроби и не является корнем какого-либо уравнения с рациональными коэффициентами.
- Связь с экспонентой: Число e является основанием натурального логарифма и имеет фундаментальную связь с понятием экспоненты. Величина e x равна значению функции экспоненты при аргументе x.
- Дифференцирование: Число e играет важную роль в дифференциальном и интегральном исчислении. Его присутствие позволяет упростить многие математические операции и уравнения.
- Равновесие: Вероятностное распределение экспоненциально распределённых случайных величин также связано с числом e.
Практическое применение
Число e имеет множество применений как в науке, так и в повседневной жизни:
- Моделирование роста и декримента популяций и состояний.
- Финансовые расчеты и проценты на кредиты.
- Калькуляция сложных процентных ставок.
- Основы теории вероятностей и статистики.
- Электрические цепи и расчеты постоянного тока.
Число e является фундаментальной константой, играющей важную роль в математике и науке. Его связь с экспонентой и дифференциальным исчислением делает его неотъемлемой частью многих математических теорий и практических приложений. Благодаря своим свойствам и значению, число e продолжает быть одной из самых изучаемых и важных математических констант в истории.
Закон радиоактивного распада
Суть закона заключается в следующем: количество нестабильных ядер вещества с течением времени уменьшается экспоненциально. Закон радиоактивного распада определяет время полураспада, которое равно времени, за которое распадается половина начального количества нестабильных ядер.
Формула закона радиоактивного распада
N(t) = N(0) * exp(-λ * t)
где:
- N(t) – количество нестабильных ядер вещества в момент времени t
- N(0) – начальное количество нестабильных ядер вещества
- λ – постоянная распада (скорость распада)
- t – время
Постоянная распада обратно пропорциональна времени полураспада и может быть вычислена по формуле:

λ = ln(2) / T1/2
где:
- ln(2) – натуральный логарифм из 2 (приблизительно равен 0.693)
- T1/2 – время полураспада
Пример применения закона радиоактивного распада
Представим, что у нас есть образец радиоактивного вещества, начальное количество ядер которого составляет 1000. Время полураспада этого вещества составляет 10 часов. Используя формулу, мы можем найти количество нестабильных ядер вещества через определенное время.
| Время (часы) | Количество нестабильных ядер |
|---|---|
| 0 | 1000 |
| 10 | 500 |
| 20 | 250 |
| 30 | 125 |
| 40 | 62.5 |
Таким образом, через 40 часов количество нестабильных ядер вещества уменьшится в 16 раз и составит 62.5.
Закон радиоактивного распада имеет широкое применение в различных областях, таких как радиоактивная датировка, медицина и промышленность. Понимание этого закона важно для изучения радиоактивности и его влияния на окружающую среду и живые организмы.
Определение числа e
Определение числа e
Число e определяется как предел последовательности (1 + 1/n) n при n, стремящемся к бесконечности. Оно также можно представить как сумму бесконечного ряда 1 + 1/1! + 1/2! + 1/3! + …. Это число является иррациональным и трансцендентным, что означает, что его нельзя представить в виде простого дробного числа или корня.
Свойства числа e
Число e обладает множеством уникальных свойств и выполняет множество математических и физических формул. Некоторые из наиболее известных свойств числа e включают:
Что же такое число е и откуда оно взялось?
Математическая константа е:
Число е является основанием натурального логарифма и обладает рядом уникальных свойств. Благодаря этим свойствам оно активно применяется во множестве различных областей, включая физику, экономику, статистику, инженерию и другие. Одним из основных свойств числа е является то, что его производная равна самому числу е:
де/dx = е
Это свойство делает число е особенно полезным для решения уравнений и задач, связанных с изменением величин во времени или пространстве.
История возникновения числа е:
Число е было введено Леонардом Эйлером в XVIII веке. Однако его происхождение уходит корнями в задачи о сложных процентах и непрерывном увеличении величин. Интересно, что первоначальное определение числа е представляло собой предел суммы (1 + 1/n) n при бесконечном увеличении значения n:
е = limit(1 + 1/n) n, при n = бесконечности

Это определение числа е связывает его с математической константой и рядом задач, связанных с непрерывным ростом и изменением величин.
Применение числа е:
Число е находит широкое применение в различных областях науки и инженерии. Некоторые из его конкретных применений включают:
- Решение дифференциальных уравнений, описывающих изменение величин во времени;
- Моделирование и прогнозирование экономических процессов;
- Расчет статистических вероятностей и доверительных интервалов;
- Проектирование электрических цепей и фильтров;
- Анализ непрерывных функций и графиков.
Число е является важным инструментом для решения сложных математических и научных задач. Оно представляет собой основу для множества математических моделей и концепций, а его свойства делают его незаменимым инструментом для анализа и моделирования различных явлений.
Примеры использования числа е:
Подводя итог, число е является одной из фундаментальных математических констант, которая находит широкое применение в различных науках и инженерии. Его происхождение уходит корнями в задачи о сложных процентах и непрерывном росте величин. Число е имеет уникальные свойства, делающие его особенно полезным для решения задач, связанных с изменением и моделированием различных явлений.
Доказательство сходимости последовательности
Определение последовательности и сходимости
Последовательность – это набор чисел, упорядоченных в определенном порядке.
Сходимость последовательности – это свойство последовательности, при котором все ее члены стремятся к определенному пределу.
Доказательство сходимости последовательности
Доказательство сходимости последовательности обычно происходит в несколько шагов:
- Формулировка предела: Необходимо явно указать предел последовательности, к которому она сходится. Обычно это число или бесконечность.
- Доказательство: Используя строгие математические операции и логику, необходимо доказать, что существует число N, такое что для всех n > N последовательность сходится к пределу.
- Выбор N: Важно выбрать подходящее значение N, чтобы доказать сходимость последовательности. Это может быть значение, полученное из начальных условий или из самих свойств последовательности.
- Доказательство ограниченности последовательности: Иногда мы можем использовать факт ограниченности последовательности для доказательства ее сходимости. Для этого нужно доказать, что все члены последовательности ограничены сверху или снизу.
- Доказательство монотонности последовательности: Если последовательность монотонна (возрастает или убывает), и ограничена сверху или снизу, то она сходится к пределу.
Пример доказательства сходимости последовательности
Рассмотрим пример доказательства сходимости последовательности:
- Формулировка предела: Доказать, что предел последовательности $a_n = frac{1}{n}$ таков, что $lim_{n to infty} a_n = 0$.
- Доказательство: Зафиксируем произвольное положительное число $varepsilon > 0$. Тогда найдется такой номер $N$, что для всех $n > N$, $|frac < varepsilon$. Так как $frac1{n} > 0$ для всех $n$, можно переписать неравенство в виде $frac{1}{n} < varepsilon$, что эквивалентно $n > frac{1}{varepsilon}$. Пусть $N = frac{1}{varepsilon}$, тогда для всех $n > N$, ${n} – 0| < varepsilon$. Таким образом, мы доказали сходимость последовательности.
- Выбор N: Для данной последовательности подходящее значение N выбирается как $N = frac{1}{varepsilon}$.
Таким образом, доказательство сходимости последовательности требует строгой логики и использования математических операций. Наличие предела, выбор подходящего значения N и использование свойств последовательности позволяют доказать ее сходимость.
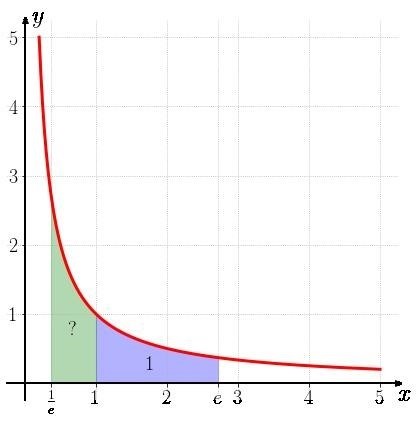
Площадь под графиком гиперболы
$$frac{x 2}{a 2} – frac{y 2}{b 2} = 1$$
График гиперболы состоит из двух отрезков, называемых асимптотами, и двух ветвей, расположенных симметрично относительно этих асимптот.
Для вычисления площади под графиком гиперболы, нужно вычислить интеграл функции, описывающей гиперболу:
$$S = int_{x_1} {x_2} left|f(x)
ight| dx$$
Где границы интеграла, $x_1$ и $x_2$, определяются точками пересечения гиперболы с осью OX.
Площадь под графиком гиперболы можно вычислить аналитически или численно, используя методы численного интегрирования.
